2014-01-25
730
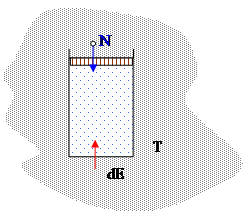
Рассмотрим дискретную систему, помещенную в термостат и имеющую пористый поршень (стенку), который позволяет обмениваться частицами с внешней системой.
Для такой системы записываем
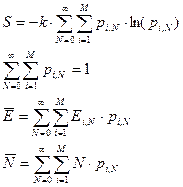. (27)
Здесь мы сменили число квантовых (дискретных состояний, вместо N пишем M).[16] Во всех формулах двойное суммирование. Число частиц в системе формально определено от 0 до бесконечности. Система уравнений дополнилась уравнением среднего числа частиц. Далее продолжаем по стандартной схеме. Записываем вариации уравнений (27)
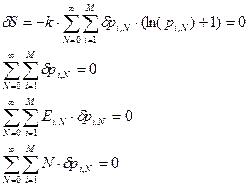. (28)
Умножаем дополнительные условия (три последних уравнения) на неопределенные множители Лагранжа a, b, g и складываем.
.
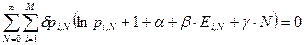Отсюда получаем функцию вероятности
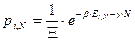. (29)
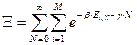- статистическая сумма большого канонического ансамбля. Очевидно, что 
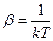. Неопределенный множитель g определим опять же методом согласования. Определим энтропию, используя полученную формулу вероятности (29).
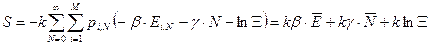. (30)
Далее используем определение термодинамического потенциала Гиббса
.
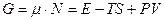Отсюда выразим энтропию
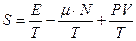. (31)
Выражения (30) и (31) содержат по три слагаемых в правых частях. Сравнивая, получаем
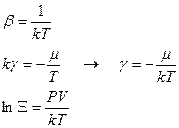. (32)
Записываем окончательное выражение для функции вероятности.
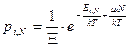. (33)
Обычно эту вероятность записывают в виде
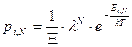. (34)
Где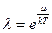 
называют абсолютной активностью. Статистическую сумму большого ансамбля, используя l можно записать в виде
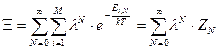. (35)
Где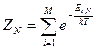 
- статистическая сумма канонического ансамбля с N частицами. Формула (32) дает основную связь статистической суммы с термодинамическими параметрами. Определим дополнительные уравнения. Для этого получим полный дифференциал логарифма большой статистической суммы, считая статистическую сумму канонического ансамбля функцией трех параметров 
.
.
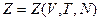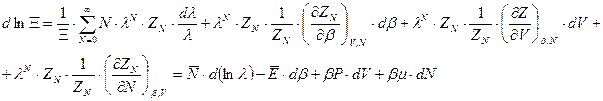Здесь мы использовали связь статистической суммы канонического ансамбля с термодинамическими параметрами (формулы (25), (26)).
Из (36) получаем
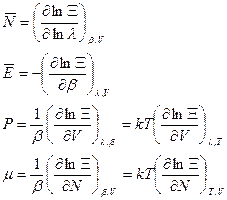. (37)
6. Функции плотности вероятности для непрерывных N – частичных классических систем. Фазовое пространство. Квазиклассическое приближение. Фазовая ячейка. Тождественность частиц.
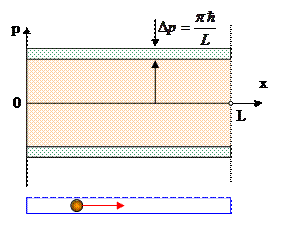
Состояние классической системы удобно показывать в фазовом пространстве – пространстве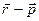 
(пространстве координат и импульсов). Первоначально рассмотрим простейший вариант системы. Рассмотрим частицу, заключенную в одномерном «ящике». Если систему считать классической, то траектории движения (состояния) в фазовом пространстве p – x представляют собой две прямые линии, соответствующие положительному и отрицательному значениям импульса. Но классическое поведение является пределом квантовых свойств системы. Энергия частицы в «ящике» квантуется.
 |
.
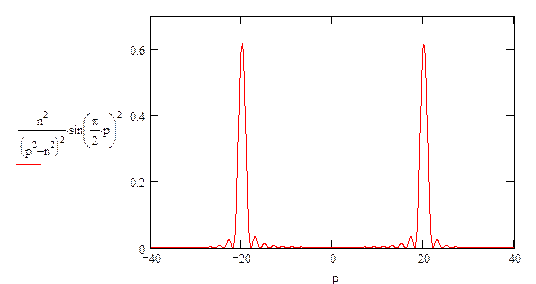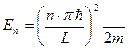Импульс не квантуется и картина состояний в фазовом пространстве не будет классически простой. Однако при больших значениях n импульс приближенно можно считать тоже квантованным. На рисунке показан импульсный спектр (функция плотности вероятности импульса) при n = 20. Видно, что даже при этом значении квантового уровня импульсный спектр можно считать дискретным.[17] Пики вероятности соответствуют двум значениям импульса
.
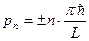При увеличении n на 1 линии импульса на фазовой плоскости передвигаются «скачком» на величину
,
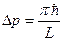тем самым, разбивая фазовую плоскость на отдельные ячейки. При этом площадь «квантовой фазовой ячейки» равна
.
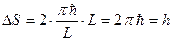Очевидно, что если область локализации частицы будет трехмерной, то размер квантовой фазовой ячейки станет равным h3.
В качестве второго примера рассмотрим одномерный квантовый осциллятор. Для получения его фазовых траекторий (в квазиклассическом приближении) запишем закон сохранения энергии с учетом квантования
.
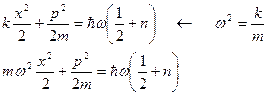Последнюю формулу можно привести к уравнению эллипса.
.
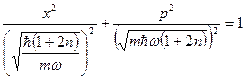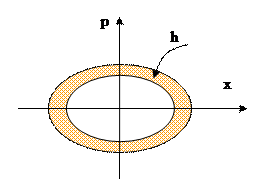
Таким образом, траектории квантовых состояний осциллятора на фазовой плоскости являются эллипсами. При этом площадь эллипса
,
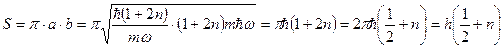(занятый «фазовый объем») растет линейно с увеличением n. Увеличение площади и в этом случае происходит дискретно на величину
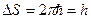. (38)
Квантовая ячейка позволяет получать число квантовых состояний, которое содержит некоторый фазовый объем.
.
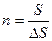Определим теперь общую форму записи дифференциальной вероятности состояния N – частичной системы (опять же в квазиклассическом приближении). Очевидно, что дифференциальная вероятность должна записываться в виде[18]
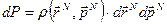. (39)
Где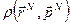 
- функция плотности вероятности. Дифференциальный объем фазового пространства 
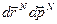с учетом представлений о его дискретности (которые мы обсудили выше) следует поделить на размер квантовой ячейки. Для N частичной системы фазовое пространство является 6 N мерным и квантовая ячейка равна h3N. После деления формула (39) принимает вид
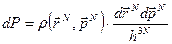. (40)
Величина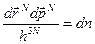 
равна числу квантовых состояний в дифференциальном фазовом объеме. Дифференциальную вероятность (40) следует уменьшить на N!, так как перестановка тождественных частиц не изменяет состояния системы. Таким образом, окончательная форма дифференциальной вероятности состояния N – частичной системы в квазиклассическом приближении запишется в виде
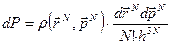. (41)
Отметим, что при такой форме функция плотности вероятности в формуле (41) является безразмерной.
