Реальные газы. Статистический интеграл реального газа с парным потенциалом. Конфигурационный интеграл. Функция Майера. Приближенный метод вычисления конфигурационного интеграла. Уравнение Ван-дер-Ваальса. Второй вириальный коэффициент.
Рассмотрим газ с парным центральным потенциалом взаимодействия. Потенциальная энергия двух частиц является функцией только расстояния между частицами.
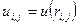 . (71)
. (71)
Статистический интеграл газа запишется в виде
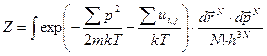 . (72)
. (72)
После интегрирования по импульсам
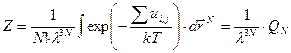 . (73)
. (73)
Интеграл
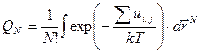 (74)
(74)
называют конфигурационным. Основная сложность теории реальных газов это сложность вычисления конфигурационного интеграла. При слабом взаимодействии и высокой температуре конфигурационный интеграл можно вычислить приближенно. Для этого разработан вычислительный прием, основанный на функции Майера
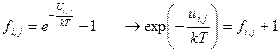 . (75)
. (75)
Использование (75) представляет полную «потенциальную» экспоненту в виде произведения
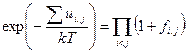 . (76)
. (76)
Поставляем (76) в (74) и аккуратно «позиционируем» интеграл
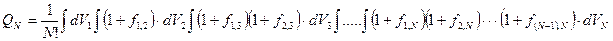
При каждом интегрировании присутствуют индексы не старше индекса дифференциала. Рассмотрим подынтегральное произведение (раскрываем его)
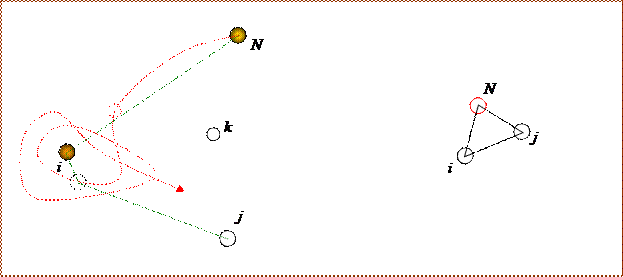
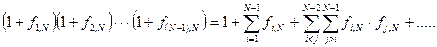 (77)
(77)
Далее этот ряд нужно интегрировать. Сложность может возникнуть при интегрировании многомерных сумм. Смысл интегрирования многомерной суммы состоит в интегрировании различных частичных конфигураций. Но при малой плотности газа можно считать «плотные» (многочастичные) комплексы маловероятными. Поэтому произведения функций Майера равны нулю. В произведении одну из функций (функцию далеких частиц) приближенно можно считать равной нулю. С учетом этого замечания ряд (77) существенно упрощается.
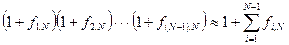 . (78)
. (78)
Конфигурационный интеграл записывается в виде
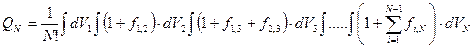 . (79)
. (79)
Рассмотрим один из интегралов
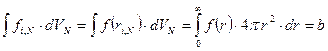 . (80)
. (80)
Очевидно, что этот интеграл от функции Майера не зависит от номеров частиц и определяется только потенциалом взаимодействия и температурой. Используя (80) конфигурационный интеграл (79) можно записать в виде
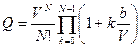 . (81)
. (81)
Статистический интеграл неидеального газа
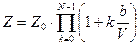 . (82)
. (82)
Это выражение можно упростить при малых величинах параметра b.
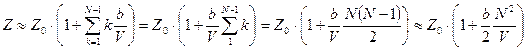 . (83)
. (83)
Теперь мы можем получить всю термодинамику неидеального газа в приближении малой плотности и высокой температуры. Свободная энергия Гельмгольца
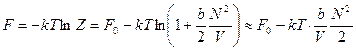 . (84)
. (84)
Термическое уравнение состояния
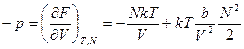 .
.
После преобразования
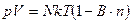 . (85)
. (85)
Здесь мы ввели обозначения
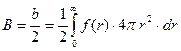 - второй вириальный коэффициент. (86)
- второй вириальный коэффициент. (86)
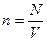 - плотность числа частиц.
- плотность числа частиц.
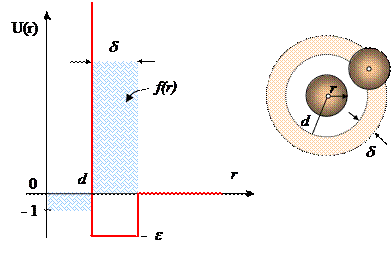 |
Вычислим второй вириальный коэффициент для конкретной модели парного потенциала. Выбираем парный потенциал в простейшем варианте потенциальной ямы. Потенциал взаимодействия имеет «жесткое ядро». Частицы являются твердыми шариками диаметра d. На небольшом расстоянии (в пределах d) частицы имеют постоянную энергию взаимодействия e. На расстояниях превышающих d + d частицы не взаимодействуют. Второй вириальный коэффициент в этом случае
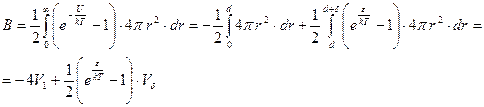 . (87)
. (87)
Будем считать показатель экспоненты e/kT малой величиной. Тогда
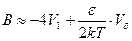 . (88)
. (88)
Подставим это «высокотемпературное» значение вириального коэффициента в термическое уравнение (85)
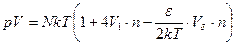 .
.
Данное уравнение можно привести к форме, известной как уравнение Ван-дер-Ваальса.
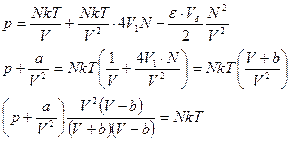 .
.
Окончательно (используя приближение 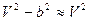 )
)
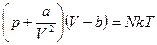 . (89)
. (89)
Где
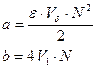 . (90)
. (90)
 Можно показать (см. последующую задачу), что величина a/V равна средней потенциальной энергии взаимодействия частиц газа. Константа b равна учетверенному собственному объему частиц («выключенному», «недоступному» объему для центров частиц газа). Уравнение Ван-дер-Ваальса было одним из первых уравнений, которое использовалось для описания состояния реальных газов.
Можно показать (см. последующую задачу), что величина a/V равна средней потенциальной энергии взаимодействия частиц газа. Константа b равна учетверенному собственному объему частиц («выключенному», «недоступному» объему для центров частиц газа). Уравнение Ван-дер-Ваальса было одним из первых уравнений, которое использовалось для описания состояния реальных газов.
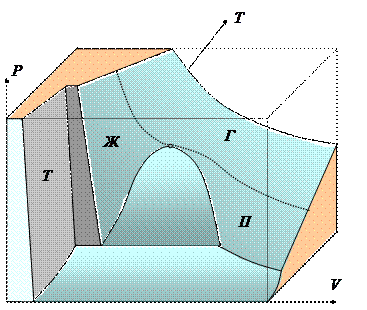
На рисунке представлена типичная фазовая диаграмма для «нормального» вещества.[24] Для различных веществ детали фазовой диаграммы могут меняться, но общая форма остается неизменной. Из рисунка видно, что поверхность P(V,T) не является «гладкой». На ней можно выделить отдельные участки (плоскости) ограниченные «изломами» поверхности. Если бы вещество было идеальным газом, то фазовая поверхность в соответствии с уравнением Клайперона-Менделеева
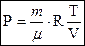
выглядела бы следующим образом[25]
 На этой диаграмме можно выделить линии «школьных» изопроцессов - законов: Гей-Люссака, Шарля, Бойля-Мариотта. Это линии сечений при постоянных параметрах: давлении, объема, температуры. При высоких температурах фазовая диаграмма реального вещества переходит в диаграмму идеального газа. При низких температурах нарушается плавность фазовой поверхности. Границами «изломов» на ней выделяются отдельные участки с качественно различными термодинамическими состояниями и различным количеством фаз.
На этой диаграмме можно выделить линии «школьных» изопроцессов - законов: Гей-Люссака, Шарля, Бойля-Мариотта. Это линии сечений при постоянных параметрах: давлении, объема, температуры. При высоких температурах фазовая диаграмма реального вещества переходит в диаграмму идеального газа. При низких температурах нарушается плавность фазовой поверхности. Границами «изломов» на ней выделяются отдельные участки с качественно различными термодинамическими состояниями и различным количеством фаз.
· Область жидкости, газа и пара (ЖГП). [26]
 Эта часть гладкой поверхности формально разделяется «критической» изотермой на три части.[27] Между этими участками нет изломов. Поэтому формально между термодинамическими состояниями: жидкости, пара и газа нет различия. Вещество плавно (изменением V и T) можно перевести из одного состояния в другое.
Эта часть гладкой поверхности формально разделяется «критической» изотермой на три части.[27] Между этими участками нет изломов. Поэтому формально между термодинамическими состояниями: жидкости, пара и газа нет различия. Вещество плавно (изменением V и T) можно перевести из одного состояния в другое.
· Двухфазная область жидкости и пара.
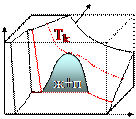 Эта область находится между двумя изотермами: критической и конечной изотермой плавления. Если в этом диапазоне температур изотермически сжимать пар (опускать поршень), то при некотором объеме на дне сосуда появится вторая фаза – жидкость. С этого момента давление в системе остается постоянным до полной конденсации пара. Дальнейшее сжатие приводит к резкому повышению давления (сжимается жидкость).
Эта область находится между двумя изотермами: критической и конечной изотермой плавления. Если в этом диапазоне температур изотермически сжимать пар (опускать поршень), то при некотором объеме на дне сосуда появится вторая фаза – жидкость. С этого момента давление в системе остается постоянным до полной конденсации пара. Дальнейшее сжатие приводит к резкому повышению давления (сжимается жидкость).
· Двухфазная область твердого тела и насыщенного пара (Т + нП).
 Эта область граничит с областью (Ж + нП) и существует ниже температуры плавления. В системе существуют две фазы: твердое тело и его насыщенный пар. Эту область называют областью сублимации (областью «сухого» испарения).
Эта область граничит с областью (Ж + нП) и существует ниже температуры плавления. В системе существуют две фазы: твердое тело и его насыщенный пар. Эту область называют областью сублимации (областью «сухого» испарения).
· Двухфазная область твердого тела и жидкости (Т + Ж).
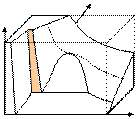 Если изотермически сжимать жидкость, то при некотором объеме в ней появляются кристаллы твердого тела, появляется вторая фаза. Эта двухфазная область существует выше температуры тройной точки. Области (Ж + нП), (Т + нП) и область (Т + Ж) в некотором смысле похожи. Поверхности этих областей цилиндрические.
Если изотермически сжимать жидкость, то при некотором объеме в ней появляются кристаллы твердого тела, появляется вторая фаза. Эта двухфазная область существует выше температуры тройной точки. Области (Ж + нП), (Т + нП) и область (Т + Ж) в некотором смысле похожи. Поверхности этих областей цилиндрические.
· Область твердого тела.
В некоторой области значений объема и температур в системе будет существовать только одна фаза – твердое тело.
· 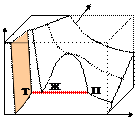 Тройная линия (линия Т-Ж-П).
Тройная линия (линия Т-Ж-П).
Если в системе точно поддерживать температуру тройной точки, то в некотором диапазоне объемов одновременно будут существовать три фазы: твердое тело, жидкость, насыщенный пар. По температуре данное состояние не является устойчивым. Небольшое изменение температуры приводит к исчезновению одной из фаз.
d Задача. Определить энергию неидеального газа (для потенциала «твердых» шариков с «ямным» потенциалом притяжения, рассмотренным выше).
Используем формулы (83) и (88).
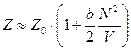
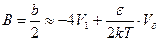
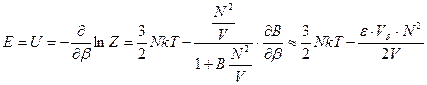 . (91)
. (91)
К энергии добавилось отрицательное слагаемое (энергия притяжения между молекулами). Структура этой добавки очевидна. 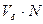 - объем энергетической области.
- объем энергетической области. 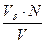 - вероятность попасть в эту область для одной молекулы (при высокой температуре). 1/2 - множитель учитывающий энергию парного взаимодействия.
- вероятность попасть в эту область для одной молекулы (при высокой температуре). 1/2 - множитель учитывающий энергию парного взаимодействия.
Сделаем замечание по поводу структуры уравнения Ван-дер-Ваальса (при данной модели потенциала).
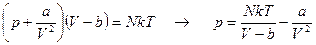
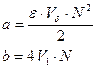
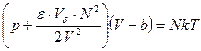 . (92)
. (92)
Отрицательная добавка к давлению равна плотности энергетической добавки к энергии газа, о которой говорилось выше. Это согласуется с энергетическим определением давления для идеального газа 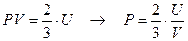 .
.
d Задача. Получить безразмерное уравнение Ван-дер-Ваальса (закон соответственных состояний).
Используем «мольное» уравнение
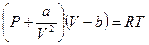 . (93)
. (93)
Для приведения к безразмерному виду используем критические параметры, которые получим методом производной. В критической точке (точке перегиба) первая и вторая производные давления по объему равны нулю.
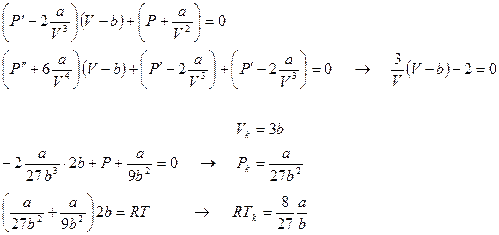 . (94)
. (94)
Введем обозначения 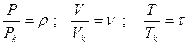 .
.
Делим уравнение (93) на критическое давление
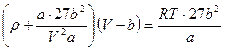 .
.
Окончательно
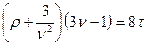 . (95)
. (95)
Рассмотрим некоторый объем заполненный равновесным тепловым излучением при температуре T. Стоячие тепловые волны можно рассматривать как квантовые гармонические осцилляторы. Будем считать отдельный квантовый осциллятор термодинамической системой погруженной в термостат. Запишем статистическую сумму такой системы.
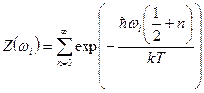 . (96)
. (96)
Здесь мы использовали формулу квантования энергии осциллятора
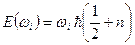 . (97)
. (97)
Статистическая сумма (96) легко вычисляется.
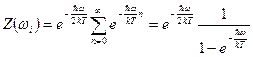 . (98)
. (98)
Определим среднюю энергию осциллятора в термостате.
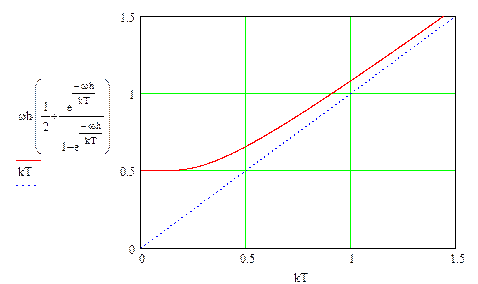
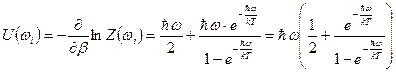 . (99)
. (99)
При абсолютном нуле энергия осциллятора равна 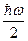 . При высоких температурах энергия становится классической
. При высоких температурах энергия становится классической 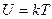 . На две степени свободы по kT/2. Полная энергия теплового излучения записывается как сумма энергий всех осцилляторов.
. На две степени свободы по kT/2. Полная энергия теплового излучения записывается как сумма энергий всех осцилляторов.
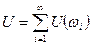 .
.
Заменим дискретное распределение частот непрерывным распределением, а сумму интегралом.
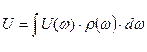 . (100)
. (100)
Для определения частотной функции плотности осцилляторов воспользуемся результатом энергетического трехмерного квантования (для частицы в «ящике»).
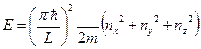 .
.
В пространстве квантовых чисел это соотношение можно представить уравнением сферы.
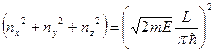 .
.
Радиус энергетической поверхности в пространстве квантовых чисел.
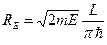 .
.
«Объем» числа состояний под энергетической поверхностью
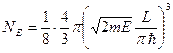 . (100¢)
. (100¢)
Число состояний на поверхности сферы в слое dE
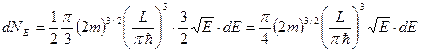 .
.
Перейдем в импульсное пространство, используя квазиклассическое приближение.
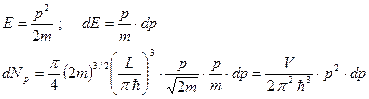 .
.
Теперь можно перейти к «фотонам» и частотам.
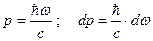 .
.
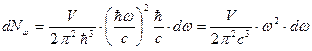 .
.
Это число состояний следует увеличить в два раза с учетом поляризации квантов.
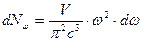 .
.
Из последней формулы получаем частотную функцию плотности числа осцилляторов
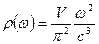 . (101)
. (101)
Используя эту формулу, записываем интеграл энергии.
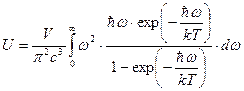 .
.
При интегрировании перейдем к новой переменной
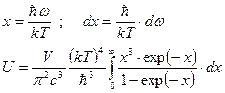 .
.
Часть подынтегральной функции можно «развернуть» в ряд.
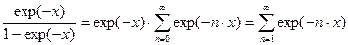 .
.
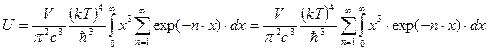
Вычислим один из интегралов ряда
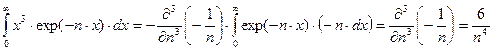 .
.
В выражении плотности энергии появляется известный ряд (приближенно равный 1, 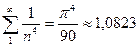 )
)
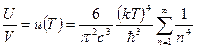 .
.
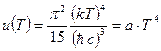 . (102)
. (102)
Получили интегральный закон Стефана-Больцмана. Плотность энергии равновесного теплового излучения пропорциональна четвертой степени абсолютной температуры. Используя формулу (101) и (99) можно записать формулу Планка, которая
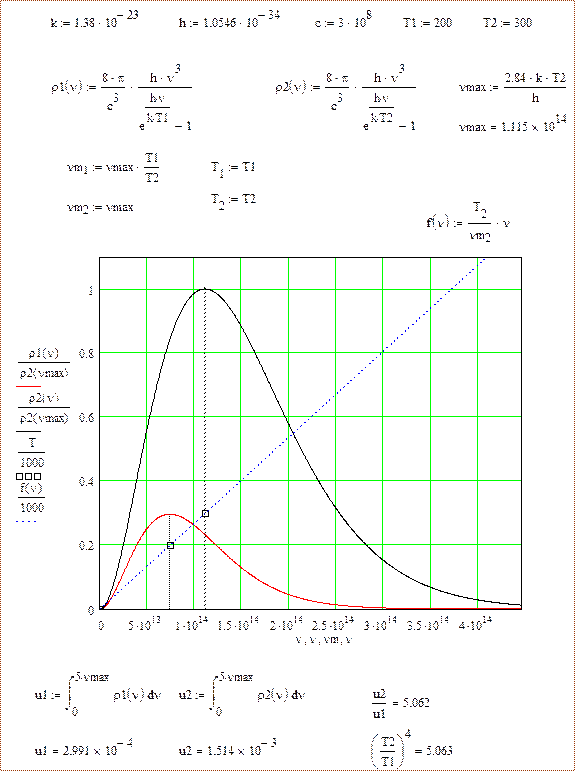 |
описывает спектральную плотность энергии.
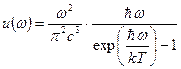 . (103)
. (103)
Функцию можно переписать для обычной частоты
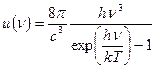 (104)
(104)
Здесь представлен листинг MathCAD, на котором построены графики спектральной плотности для двух температур (200 и 300 К). При построении графиков функцию плотности нормировали на максимальное значение второго графика. Для этого было использовано приближенное значение частоты максимума (см. ниже). Здесь же на общем графике показан линейный закон Вина.
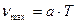 . (105)
. (105)
Частота, соответствующая максимуму распределения пропорциональна температуре. Этот закон легко получить дифференцированием функции распределения.
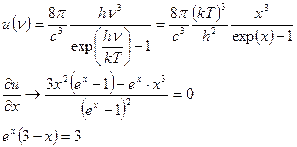 .
.
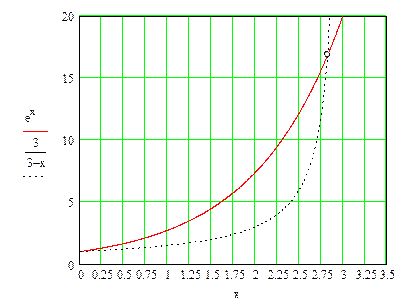 |
Приближенное решение трансцендентного уравнения
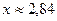 .
.
Это графическое решение, полученное в MathCAD.
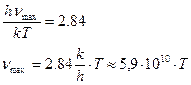 . (106)
. (106)
Закон Вина обычно записывают через длину волны. Для этого нужно переписать спектральную плотность в «волновом» виде (учитывая 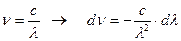 ).
).
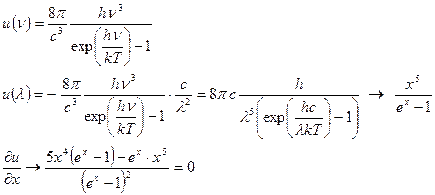 .
.
Уравнение, определяющее максимум «волновой» функции плотности.
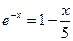 . Приближенное решение этого уравнения
. Приближенное решение этого уравнения 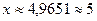 .
.
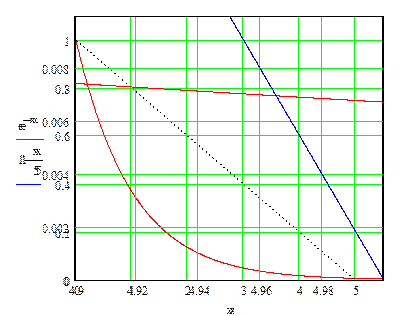 |
Графическое решение трансцендентного уравнения 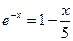 .
.
Закон «смещения Вина» для длины волны соответствующей максимуму функции распределения.
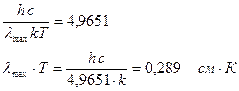 . (107)
. (107)
d Задача. Получить закон Стефана-Больцмана «термодинамическим» методом.
Используем формулу давления излучения на поглощающую стенку 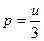 и уравнение энергии
и уравнение энергии 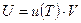 . Далее записываем первый закон термодинамики
. Далее записываем первый закон термодинамики
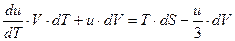 .
.
Выделим полный дифференциал энтропии
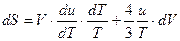 .
.
Для полного дифференциала справедливо («перекрестные» производные дифференциальных множителей равны)
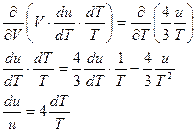 .
.
Интегрируем последнее соотношение и получаем закон Стефана-Больцмана.
 .
.
 2014-01-25
2014-01-25 911
911








