7.1 Прямолинейное движение точки с постоянной скоростью.
Предположим, что скорость прямолинейного движения постоянна. Следовательно 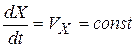 . Выразим из предыдущего уравнения
. Выразим из предыдущего уравнения 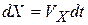 и проинтегрируем это выражение:
и проинтегрируем это выражение: 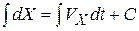 , где С — произвольная постоянная интегрирования. Интегралы в данном уравнении относятся к числу простейших (
, где С — произвольная постоянная интегрирования. Интегралы в данном уравнении относятся к числу простейших (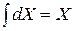 ,
,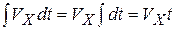 ), поэтому легко получаем зависимость координаты Х от времени t:
), поэтому легко получаем зависимость координаты Х от времени t: 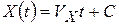 . Так как при t =0 материальная точка находилась в положении
. Так как при t =0 материальная точка находилась в положении 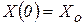 , то
, то 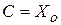 . Следовательно, закон прямолинейного движения с постоянной скоростью имеет вид:
. Следовательно, закон прямолинейного движения с постоянной скоростью имеет вид: 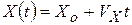 .
.
7.2 Прямолинейное движение точки с постоянным ускорением.
В этом случае сначала необходимо найти закон движения для скорости. Так как при прямолинейном движении ускорение есть первая производная от скорости, то можем записать: 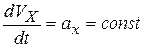 . Выражаем
. Выражаем 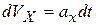 и интегрируем по времени t в пределах от
и интегрируем по времени t в пределах от 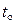 до t. Получим
до t. Получим 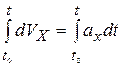 . В результате получим, что
. В результате получим, что 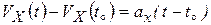 , или
, или 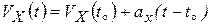 .
.
Повторяя процедуру, показанную в п. 7.1, получим закон движения при равноускоренном прямолинейном движении:
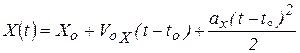 .
.
 2014-01-25
2014-01-25 929
929








