Описание кругового движения координатным способом

Определение 3

За положительное направление изменения угла принимается направление его возрастания при движении точки 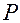против часовой стрелки, если смотреть с конца вектора 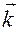оси 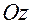на плоскость .

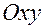Положение точки 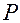на окружности можем задать через радиус 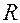и угол по следующим формулам:

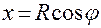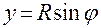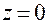, , . (1.3.1)

Движение точки 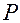будет задано, если укажем закон изменения угла от времени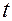

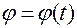, (1.3.2)

поскольку при круговом движении, согласно определению 2, выполняется тождество по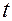

.

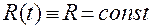Таким образом, круговое движение можем задать в виде

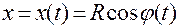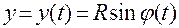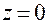, , . (1.3.3)

Формулы (1.3.3) дают координатный способ задания движения.

3º. Векторный способ задания кругового движения