Закон движения по окружности

В формуле (1.3.6)

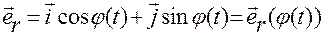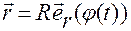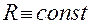, ,(1.3.6)

вектор-функция 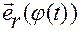строится через угол , отсчитываемый от положительного направления оси 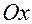в плоскости движения материальной точки. Возможны и другие способы построения этой функции.

Например, можно задавать ее значения в зависимости от длины дуги окружности.

В естественном способе закон движения по траектории задается в виде

,

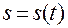где 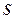– длина дуги траектории.

Будем отсчитывать длину дуги окружности от точки 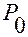пересечения окружности с осью 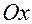(см. рис.1.3.2). Положительное направление отсчета длины дуги считаем совпадающим с положительным направлением отсчета угла .

Тогда, как известно из геометрии, длина 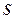дуги 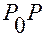выражается через угол соотношением

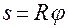. (1.3.7)

Подставляя в (1.3.7) закон движения, задаваемый в форме (1.3.2)

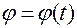, (1.3.2)

получаем

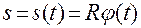. (1.3.8)

Формула (1.3.8) дает закон движения точки 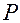по окружности в естественной параметризации.