Пример 1
Примеры криволинейных координат
Положение точки 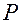 задается переменными
задается переменными 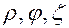 (см. рис.1.5.1).
(см. рис.1.5.1).
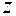
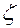
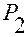 (
(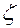 )
)




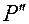
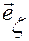 (
(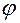 )
)



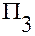
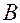
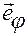


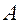
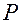

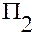
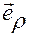
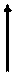
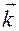
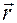
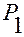
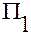 (
(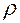 )
)








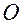
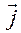
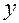

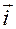
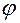
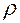
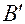
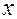
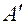
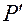
Рис.1.5.1
Переменные 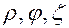 имеют следующий геометрический смысл:
имеют следующий геометрический смысл:
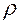 — расстояние от полюса
— расстояние от полюса 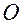 до проекции точки
до проекции точки 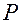 на плоскость
на плоскость 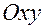 .
.
Его значения удовлетворяют неравенству:
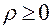 .
.
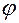 — угол в плоскости
— угол в плоскости 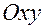 , отсчитываемый от положительного направления оси
, отсчитываемый от положительного направления оси 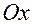 до луча
до луча 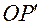 .
.
Здесь 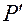 — это проекция точки
— это проекция точки 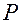 на плоскость
на плоскость 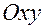 .
.
Угол 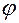 принимает значения из промежутка
принимает значения из промежутка
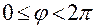 .
.
Положительное направление отсчета угла 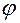 задается правилом правой руки.
задается правилом правой руки.
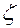 — проекция радиус-вектора
— проекция радиус-вектора 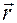 точки
точки 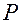 на ось
на ось 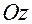 ;
;
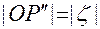 , где
, где 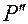 — проекция точки
— проекция точки 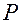 на ось
на ось 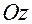 .
.
Переменная 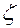 может принимать любые значения
может принимать любые значения
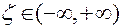 .
.
Связь декартовых прямоугольных координат 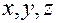 точки
точки 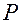 с цилиндрическими задается следующими формулами:
с цилиндрическими задается следующими формулами:
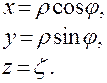
Обратная зависимость 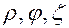 от
от 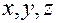 , т.е. связь цилиндрических координат с декартовыми, имеет вид:
, т.е. связь цилиндрических координат с декартовыми, имеет вид:
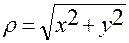 ,
, 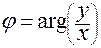 ,
, 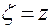 .
.
Если
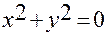 ,
,
то аналогичным образом можно ввести цилиндрические координаты 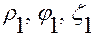 по отношению к системе координат
по отношению к системе координат 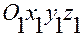 , у которой, например, полюс
, у которой, например, полюс 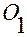 смещен вдоль оси
смещен вдоль оси 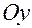 , ось
, ось 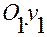 совпадает с осью
совпадает с осью 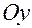 , а оси
, а оси 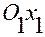 и
и 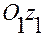 коллинеарны осям
коллинеарны осям 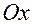 и
и 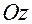 , соответственно.
, соответственно.
В тех случаях, когда движения точки могут приводить ее на ось 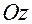 , следует переходить к описанию этих движений в переменных
, следует переходить к описанию этих движений в переменных 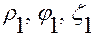 .
.
 2014-01-25
2014-01-25 933
933








