“Кристаллы блещут симметрией”, ¾ утверждал Е.С. Федоров в классическом “Курсе кристаллографии” и так определил это понятие: «Симметрия есть свойство геометрических фигур … в различных положениях приходить в совмещение с первоначальным положением». В переводе с греческого языка “симметрия” означает “соразмерность”. Симметричной называется фигура, которая может совместиться сама с собой в результате некоторых преобразований¾ отражений и вращений, именуемых операциями симметрии. Операции симметрии осуществляются с помощью вспомогательных геометрических образов ¾ элементов симметрии, представляющих собой воображаемые плоскости, линии и точки.
Для обозначения симметричных преобразований и соответствующих им элементов симметрии в кристаллографии используют условные символы. Существуют несколько систем обозначений, но наиболее распространены две из них. Одна из них основана на формулах симметрии и часто используется в геометрической кристаллографии. Другая, международная символика, принята Интернациональным союзом кристаллографов. Обозначения элементов симметрии в обеих символиках приведены в табл. 1.
Полный перечень элементов симметрии позволяет составить полное представление о всех симметричных преобразованиях, возможных в данной геометрической фигуре. Весь этот перечень представлен в формуле симметрии, которая содержит записанные в установленном порядке все элементы симметрии описываемого объекта. Принятый порядок их расположения в формуле следующий: оси симметрии от высших к низшим, затем плоскости симметрии и в завершение ¾ центр симметрии.
Таблица 1. Обозначение элементов симметрии конечных фигур
|
Название элемента симметрии | Обозначение
| |
| международный (интернациональный) символ | по формуле симметрии | |
| Плоскость симметрии | m | P |
| Центр симметрии | 1 | C |
| Поворотная ось симметрии: | n | Ln |
| второго порядка, двойная | 2 | L2 |
| третьего порядка, тройная | 3 | L3 |
| четвертого порядка, четверная | 4 | L4 |
| шестого порядка, шестерная | 6 | L6 |
| Инверсионные оси симметрии: | n | Ln = Lni |
| Третьего порядка | 3 | L3 = L3i |
| четвертого порядка | 4 | L4 = L4i |
| шестого порядка | 6 | L6 = L6i |
Плоскости симметрии
Плоскостью симметрии называется такая плоскость, которая делит фигуру на две зеркально-равные части, расположенные относительно друг друга как предмет и его зеркальное отражение (рис. 1.5).
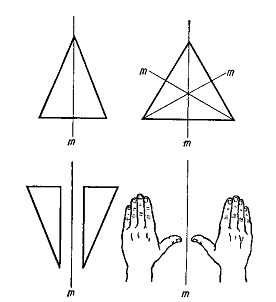
Рис. 1.5. Примеры действия плоскостей симметрии
Например, в кубе три взаимно перпендикулярные плоскости симметрии делят пополам его противоположные ребра (рис. 1.6,а). Шесть других плоскостей симметрии проходят по диагоналям граней куба (рис.1.6, б, в). Все девять плоскостей симметрии пересекаются в одной точке ¾ в центре куба.
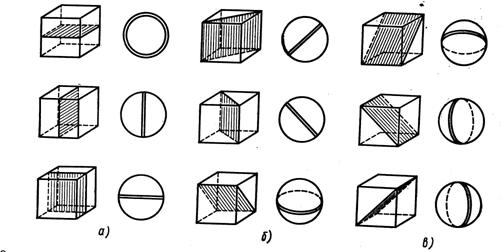
Рис. 1.6. Плоскости симметрии куба
Все плоскости симметрии геометрической фигуры пересекаются друг с другом. Коэффициент перед символом плоскости симметрии P в формуле показывает число этих плоскостей.
Оси симметрии
Осью симметрии называется воображаемая прямая линия, проходящая через середину фигуры, при повороте вокруг которой на некоторый определенный угол фигура совмещается сама с собой. Наименьший угол поворота, приводящего фигуру в самосовмещение, называется элементарным углом поворота a.
Порядок оси симметрии n показывает сколько раз фигура совмещается сама с собой при полном повороте на 3600 вокруг данной оси. Для произвольных геометрических фигур в природе возможны оси симметрии любого порядка от первого до бесконечного. В принципе, всякая фигура, повернутая вокруг любого направления на 3600, совмещается сама с собой и, следовательно, обладает бесконечным количеством осей симметрии первого порядка. Например, у кругового конуса имеется одна ось симметрии бесконечного порядка. Через нее проходит бесконечное число плоскостей симметрии.
По-иному обстоит дело с решетчатыми системами, в частности, с кристаллами.
У кристаллов невозможны оси симметрии пятого и выше шестого порядков.
Это требование является следствием решетчатого строения кристаллов. Структуры кристаллов схематично можно представить себе состоящими из параллельно ориентированных правильных параллелепипедов. Для того чтобы заполнять пространство полностью такие параллелепипеды должны иметь только двойные, тройные, четверные или шестерные оси симметрии. Параллелепипеды с осями пятого и выше шестого порядков заполняют пространство, оставляя пустоты между отдельными параллелепипедами. Пятерная ось и оси седьмого, восьмого и выше порядков несовместимы с расположением узлов в решетчатых системах. Внутренняя симметрия кристаллов соответствует симметрии их внешней формы и соответственно этому доказывается невозможность у кристаллов осей симметрии пятого и выше шестого порядков.
В качестве примера на рис. 1.7 дана схема пространственного соотношения осей симметрии кубического многогранника. У куба есть три оси четвертого порядка L4, проходящие через центры противолежащих граней, четыре оси третьего порядка L3 вдоль его пространственных диагоналей и шесть осей второго порядка L2, соединяющие середины противоположных пар ребер. Все оси пересекаются в центре фигуры.
Рис. 1.7. Оси симметрии куба: а) 3 L4; б) 4 L3; в) 6 L2;
Коэффициенты перед символом оси симметрии показывает число осей данного порядка симметрии в кубе.
Центр симметрии
Центр симметрии (центр инверсии) ¾ особая точка внутри фигуры, характеризующаяся тем, что любая проведенная через нее прямая, встречает на равных расстояниях одинаковые (соответственные) точки этой фигуры по обе стороны от центра.
Примеры геометрических фигур, обладающих центром симметрии, приведены на рис. 1.8. В процессе симметричного преобразования в центре симметрии каждая точка фигуры отражается в нем таким образом, что фигура поворачивается при этом “с лица наизнанку”. При наличии центра симметрии каждой грани кристаллического многогранника отвечает другая грань, равная и обратно параллельная первой. В частности, равны и обратно параллельны два треугольника, показанные на рис. 1.8, в.
Рис.1.8. Действие центра симметрии
Обратная параллельность – характеристический признак фигур, обладающих центром инверсии.
В кубе центр симметрии совпадает с геометрическим центром куба. С учетом осей и плоскостей симметрии формула симметрии куба имеет вид 3L44L36L29PC.
 2018-03-08
2018-03-08 599
599








