Доверительная вероятность

Одна из основных задач выборочного исследования состоит в том, чтобы на основе характеристик выборочной совокупности получить достоверные суждения об этих характеристиках в генеральной совокупности. Возможные расхождения между характеристиками выборочной и генеральной совокупности измеряются разностью между значением характеристики в генеральной совокупности и ее значением, вычисленным по результатам выборочного наблюдения. Так, для средней арифметической, это расхождение определяется по формуле

. (2.3)

Зная выборочную среднюю величину признака () и предельную ошибку выборки (), можно определить границы, в которых заключена генеральная средняя:

. (2.4)

Интервал () получил название доверительного интервала, а величины и - доверительных границ. Вероятность того, что случайный интервал () содержит в себе достоверную, но не известную наблюдателю характеристику 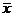, получила название доверительной вероятности . Вероятность характеризует надежность статистической оценки .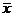

Функция в Excel ДОВЕРИТ рассчитывает значение предельной ошибки выборки и имеет следующий синтаксис

ДОВЕРИТ(альфа; станд_откл; размер).

Аргументы функции имеют следующее назначение:

альфа – уровень значимости, который связан с надежностью (доверительной вероятностью) зависимостью . Если получаем результат надежностью в 95%, то =1-0,95=0,05;

станд_откл – стандартное отклонение генеральной совокупности;

размер – размер выборки.

Пример 2.2 В результате выборочного обследования жилищных условий жителей города, получены результаты сведенные в таблицу 2.2. Требуется с уровнем надежности =95% определить границы интервала, в который попадает средний размер общей площади.

Таблица 2.2

общая площадь, приходящаяся на 1 человека, кв.м	До 5	5-10	10-15	15-20	20-25	25-30	30 и более
число жителей	8	95	204	270	210	130	83

Решение задачи приведено в таблицах 2.3 и 2.4.

Для использования функции ДОВЕРИТ необходимо вычислить три аргумента.

Аргумент альфа вычисляется по исходной надежности =1-0,95=0,05.

Для вычисления стандартного отклонения для генеральной совокупности можно воспользоваться формулой (1.4) расчета взвешенной дисперсии.

Однако, если неизвестно значение математического ожидания 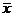, расчет дисперсии ведется по средней арифметической и формула для расчета будет иметь вид

. (2.5)

По исходным данным были определены середины интервалов.

Было определено число жителей в выборочной совокупности n как сумма строки «число жителей» f.

Для оценки выборочной средней арифметической применена функция (1.3).

При этом использовалась функция СУММПРОИЗВ, которая перемножила два массива данных – строки «середина интервала» x и «число жителей» f.

Отдельно определены разности квадратов для каждого интервала, где - середина интервала.

После этого была определена , где также использована функция СУММПРОИЗВ, далее вычислено , для чего применена функция КОРЕНЬ.

Предельная ошибка выборки определена функцией ДОВЕРИТ, где последний аргумент – размер выборки уже известен () и аргументы функции будут

ДОВЕРИТ().

После определения предельной ошибка выборки легко вычислить определить границы интервала, в который попадает средний размер общей площади, приходящейся на одного человека в городе. Это от 18,56 до 19,45 квадратных метра. Надежность этого вывода не хуже 95%.

Таблица 2.3

общая площадь, приходящаяся на 1 человека, кв.м

середина интервала, x

число жителей, f

До 5

2,5

272,42

5-10

7,5

132,37

10-15

12,5

204

42,32

15-20

17,5

270

2,27

20-25

22,5

210

12,22

25-30

27,5

130

72,17

30 и более

32,5

182,12

Таблица 2.4

Число жителей в выборочной совокупности		1000
Выборочная средняя		19,01
Генеральная дисперсия		51,11
Генеральная стандартное отклонение		7,15
Предельная ошибка выборки		0,44
Нижняя граница		18,56
Верхняя граница		19,45