Обчислення моментів інерції тіл різної форми відносно симетричних осей

     ІV. КОРОТКІ ТЕОРЕТИЧНІ ВІДОМОСТІ

     У випадку обертового руху роль маси, що виступає в рівняннях поступального руху, відіграє момент інерції.

     Моментом інерції тіла відносно деякої осі називається сума моментів інерції всіх точок (m_ir_i ²) цього тіла відносно цієї осі:

                                           .                                 (11.1)

     Якщо розподіл густини однорідний, то dm =r× dV і момент інерції можна обчислити за формулою:

.                                     (11.2)

     При обертанні тіла навколо закріпленої точки виконується рівняння (моментів)

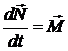                                           ,                                                (11.3)
де 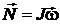 – сумарний момент імпульсу твердого тіла відносно точки закріплення, а  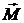– сумарний момент сили відносно цієї ж точки. В цьому випадку J є тензором інерції:

.                                 (11.4)

У випадку, коли головні осі тіла співпадають з осями координат тензор інерції приводиться до діагонального вигляду:

.                                 (11.5)

     V. МЕТОДИКА ЕКСПЕРИМЕНТУ

     Механічна конструкція приладу РМ-05 показана на рис. 11.1. На основі (2) закріплений мілісекундомір РМ-14 (1) і колона (3), на якій з допомогою притискних гвинтів закріплені кронштейни (4, 5, 6). Кронштейни (4, 6) мають гвинтові затискувачі, що закріплюють стальний дріт, на якому підвішена рамка (7). На кронштейні (5) закріплена стальна плита (8), яка є основою фотоелектричного датчика (9), електромагніта (10) та кругової кутової шкали (11). Електромагніт (10) може змінювати своє положення на плиті, а його положення відносно фотоелектричного датчика вказує на кутовій шкалі стрілка, прикріплена до електромагніту.

     Конструкція рамки (7) дозволяє закріплення в ній досліджуваних тіл (12), які можуть значно відрізнятися один від одного зовнішніми розмірами. Тіла закріплюються за допомогою рухомої горизонтальної балки, яка переміщується вздовж нерухомих вертикальних направляючих рамки. Балка фіксується шляхом закручування гайок на затискних втулках, розташованих на ній. Фотоелектричний датчик і електромагніт з’єднані з мілісекундоміром. За допомогою даної установки визначають моменти інерції та еліпсоїди інерції твердих тіл за методом крутильних коливань.

     Встановимо залежність між величинами моментів інерції тіла для осей обертання, які пересікаються в одній точці, визначимо момент інерції тіла відносно деякої осі обертання ОА (рис. 11.2). За початок координат вибрана довільна точка, яка знаходиться в тілі на цій осі. З осями координат вісь обертання ОА складає кути a, b, g. Тоді момент інерції тіла відносно цієї осі ОА буде

                          (11.6)

                                      Рис. 11.1

              рис. 11.2                                              рис. 11.3

Оскільки r²= x ²+ y ²+ z ², OB = x ×cosa+ y ×cosb+ z ×cosg і врахувавши, що cos²a+cos²b+cos²g=1, одержимо після відповідних перетворень:

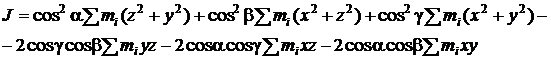
Вирази при квадратах косинусів кутів – це моменти інерції тіла відносно осей координат x, y, z  (завжди додатні):

              ; ; ,

а інші:

              ; ;

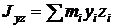називають відцентровими моментами інерції (вони можуть бути додатними, від’ємними або рівними нулеві). В загальному випадку момент інерції визначається не однією величиною, а шістьма величинами. Для різних осей (кути a, b, g – різні) величини моментів інерції будуть різними.

     Розглянемо геометричну інтерпретацію зміни величини моменту інерції тіла в залежності від положення вибраних осей обертання тіла. Для цього відкладаємо від початку координат 0 вздовж осей в довільному, але однаковому масштабі, відрізки , де J_i - момент інерції тіла відносно і -ої вибраної осі. Кінці всіх відрізків (OD)_і створюють деяку поверхню. Яке рівняння цієї поверхні? Запишемо координати кінця будь-якого відрізка OD: x = OD cosa, y = OD cosb, z = OD cosg, звідси , , . Підставивши позначення J_x=A, J_y=B, J_z=C, J_yz = D, J_zx=E, J_xy=F, одержимо шукане рівняння поверхні

Ax ² + By ² + C z ² – 2 Dyz – 2 Ezx – 2 Fxy – 1 = 0.          (11.9)

Така поверхня називається еліпсоїдом інерції відносно точки 0. Осі еліпсоїда інерції називаються головними осями інерції тіла відносно вибраної точки 0. Рівняння еліпсоїда відносно системи координат, осі якої співпадають з головними осями не містить членів з добутками різних координат:

J_x × x ² + J_y × y ² + J_z × z ².                                  (11.10)

Еліпсоїд інерції відносно центра тяжіння тіла називають центральним, а його головні осі називають головними центральними осями інерції. Для однорідних симетричних тіл головні центральні осі інерції є також і осями симетрії тіла.

     Знаючи поверхню (еліпсоїд інерції), можна завжди визначити момент інерції тіла відносно будь-якої іншої, не головної осі, що проходить через початок координат (вибрану точку 0), оскільки

                   J = 1/(OD)² = J_x cos²a + J_y cos²b + J_z cos²g.           (11.11)

     Для крутильних коливань момент інерції визначається за формулою

                                           ,                                   (11.12)

де T - період коливань,   k - модуль кручення,

,                                            (11.13)

l - довжина дротини, r - її радіус, G - модуль зсуву.

     За формулами (11.12) та (11.13) можна визначити момент інерції пустої рамки J ₀ та рамки з досліджуваним тілом 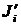 відносно вибраних осей обертання. Момент інерції тіла J_i відносно і -ої осі визначається за допомогою виразу:

.                            (11.14)

У цій формулі T_i – період крутильних коливань рамки з тілом відносно і -ої осі, T ₀  - період коливань пустої рамки відносно цієї ж осі.

     Модуль кручення k можна відшукати, не тільки використовуючи формулу (11.13), але також опираючись на експериментальне і теоретичне дослідження моменту інерції куба в даній роботі.

     Відомо, що момент інерції куба відносно будь-якої осі, що проходить через центр мас, визначається за формулою:

                         J _куба  = ma ²/6,                                         (11.15)

де m - маса куба, a - довжина ребра куба. Еліпсоїд інерції у цьому випадку перетворюється у сферу. До речі, випадок з кубом добре ілюструє принцип симетрії Неймана: симетрія властивості, у даному випадку тензора (моменту інерції), може бути вищою, ніж симетрія твердого тіла. І справді, симетрія сфери інерції вища за симетрію куба.

     Експериментальна формула для знаходження моменту інерції куба записується:

                        .               (11.16)

Із формул (11.15) і (11.16) одержуємо вираз для знаходження k:

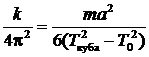                             .                               (11.17)

Підставляючи (11.17) в (11.14), одержуємо:

                                  .                               (11.18)

Ця формула справедлива для тіла будь-якої форми. Якщо тіло має форму паралелепіпеда (рис.11.3), сторони якого рівні a (вздовж осі 0X), b (вздовж осі 0Y) і c (вздовж осі 0Z), то у формулі (11.11), якщо вісь обертання вибрана вздовж діагоналі (i = d), косинуси відповідних кутів обчислюються за формулами:

; ; .  (11.19)

Тоді, підставивши у формулу (11.11) вирази (11.19) і (11.16), одержуємо:

.                                 (11.20)

При виводі формули (11.20) враховано, що індекс i у формулі (11.18) приймає значення d, x, y, z; T _x, T _y, T _z, T _d - період крутильних коливань відносно осей 0X, 0Y, 0Z і АА (діагоналі, див. рис.11.3) відповідно, які знаходяться експериментально.

     Рівняння (11.20) перевіряється експериментально у даній лабораторній роботі. Формули (11.18) і (11.20)  є робочі формули.

     VI. ПОРЯДОК ВИКОНАННЯ РОБОТИ

     1. Вимірюють розміри досліджуваних тіл a, b, c в різних місцях з допомогою штангенциркуля не менше 5 разів. Результати обробляють за схемою № 1.

     2. Рамку приладу повертають, наблизивши її стрілку до електромагніту таким чином, щоб електромагнітна сила фіксувала положення рамки. Натиснути кнопку “ПУСК” і, відрахувавши не менше n=10 крутильних коливань, натиснути кнопку “СТОП” фіксуючи час коливань t. За формулою T = t /n знайти період коливань рамки Т ₀.

     3. Закріплюють в рамці сталевий куб. В середині кожної грані зроблені невеликі заглиблення, які дозволяють закріплювати куб (так само і паралелепіпед – див. нижче) при обертанні навколо осей 0Х, 0Y, 0Z. Крім того заглиблення зроблені в місцях, які дозволяють закріплювати тіло так, щоб воно могло обертатися відносно діагоналей куба (паралелепіпеда, АА на рис. 11.3). Почергово змінюючи положення куба відносно осей, провести вимірювання, як описано в попередньому пункті, визначивши періоди коливань T _x, T _y, T _z, T _d. Переконуються, що T _куба= T _x= T _y= T _z. Результати обробляють за схемою № 1.

     4. Для знаходження маси куба m достатньо провести одне зважування на технічних терезах.

     5. Використовуючи формулу (11.17), знайти модуль кручення. За формулою (11.13) обчислити значення модуля кручення і порівняти одержані результати.

     6. Замінюють куб паралелепіпедом. Визначають для різних його положень (так як в п.2) періоди коливань T _x, T _y, T _z, T _d. Обробку результатів вимірювань проводять за схемою №1.

     7. Перевіряють правильність рівності (11.20): порівнюють значення періодів T _d, одержані з досліду і за формулою (11.20), враховуючи похибки вимірювань. В цьому випадку використовують схему №4.

     8. За формулою (11.18) обчислюють моменти інерції досліджуваних тіл відносно осей 0X, 0Y, 0Z  та діагоналі, вираховуючи похибки за схемою №4.

     9. За відомими моментами інерції будують еліпсоїди інерції для досліджуваних тіл.

     10. Проводять аналіз одержаних результатів і роблять короткі висновки.