Случай 1. Если функция в интеграле нечётная относительно косинуса, то есть  , нужна замена:
, нужна замена:  .
.
Докажем, что эта замена сводит к рационалной дроби относительно t.
 .
.
Далее,  , поэтому
, поэтому  .
.
Таким образом, будет корень в нечётной степени, полученный при замене в самой функции, и ещё один - из дифференциала. А если корень нечётной степени или умножить, или поделить на ещё один, то в итоге получится корень в чётной степени, то есть просто целая степень от  , т.е. какой-то многочлен от
, т.е. какой-то многочлен от  . Таким образом, эта замена сводит всё к целым степеням от
. Таким образом, эта замена сводит всё к целым степеням от  .
.
Пример. Вычислить интеграл  .
.
Решение. Видим, что здесь функция нечётная относительно косинуса, то есть  . Поэтому применим замену
. Поэтому применим замену  .
.
В этом случае  ,
,  ,
,  .
.
 =
=  . Нечётная степень этого корня сократится с одним дополнительным корнем, который появился при пересчёте дифференциала, и станет чётная степень корня квадратного.
. Нечётная степень этого корня сократится с одним дополнительным корнем, который появился при пересчёте дифференциала, и станет чётная степень корня квадратного.
 =
= 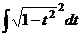 =
=  .
.
Знак модуля здесь вовсе не нужен, ведь  с областью значений
с областью значений  , так что заведомо выполняется
, так что заведомо выполняется  .
.
 =
=  =
= 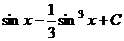 .
.
Случай 2. Нечётная относительно sin функция в интеграле, то есть выполняется свойство  . Тогда замена:
. Тогда замена:  .
.
В этом случае  ,
,  ,
,  .
.
В результате тоже получается корень  в чётной степени.
в чётной степени.
Случай 3. Если при смене знака и синуса, и косинуса знак итогового выражения по меняется 2 раза, то есть останется прежним.

Это означает, что суммарная степень чётна. Замена:  .
.
 , соответственно,
, соответственно, 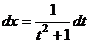 .
.
Докажем, что все выражения с sin и cos сводятся к рациональной дроби.
ДОК 5 (Л2).
Доказать, что если функция нечётна относительно косинуса, замена  сводит интеграл к рациональной дроби, а если
сводит интеграл к рациональной дроби, а если  то замена
то замена  сводит интеграл к рациональной дроби.
сводит интеграл к рациональной дроби.
Выразим синус и косинус.  . Нужно выразить синус того угла, тангенс которого равен t. Рассмотрим прямоугольный треугольник, обозначим противолежащий и прилежащий катеты: t и 1. Но тогда по теореме Пифагора, гипотенуза равна
. Нужно выразить синус того угла, тангенс которого равен t. Рассмотрим прямоугольный треугольник, обозначим противолежащий и прилежащий катеты: t и 1. Но тогда по теореме Пифагора, гипотенуза равна  . Подпишем её тоже.
. Подпишем её тоже.

А теперь можно выразить синус и косинус:
 ,
,  .
.
Пример. Вычислить интеграл 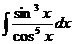 .
.
Решение. Степени обеих функций нечётны, суммарная степень чётна. То есть, это как раз тот случай, когда можно сделать замену  .
.
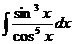 =
=  =
=  =
=
 =
=  =
=  =
= 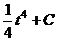 =
=  .
.
Ответ.  .
.
 2018-03-09
2018-03-09 136
136








