Сейчас мы наичимся интегрировать выражения, содержащие 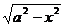 ,
, 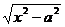 , или
, или 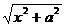 . Эти иррациональности сводятся к тригонометрическим функциям.
. Эти иррациональности сводятся к тригонометрическим функциям.
Случай 1. 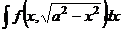 .
.
Замена: 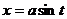 (или
(или 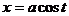 ).
).
Рассмотрим замену 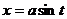 . На самом деле надо было записать
. На самом деле надо было записать  , ведь по идее, для замены надо вводить новую переменную и выражать её через старую. Однако, запомнить здесь вам будет легче именно «обратную» замену в виде
, ведь по идее, для замены надо вводить новую переменную и выражать её через старую. Однако, запомнить здесь вам будет легче именно «обратную» замену в виде 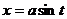 .
.
Далее получается 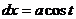 , а корни в этом выражении исчезают так:
, а корни в этом выражении исчезают так:  =
= 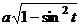 =
= 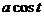 . Таким образом, всё сводится к тригонометрическим функциям.
. Таким образом, всё сводится к тригонометрическим функциям.
Пример. Вычислить интеграл  .
.
Здесь 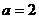 , потому что
, потому что 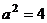 .
.
Замена 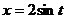 . Корень при этом превратится в
. Корень при этом превратится в 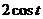 .
.
Итак,  =
= 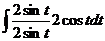 =
= 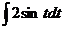 =
= 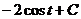 .
.
после обратной замены, это  .
.
Можем упростить композицию прямой и обратной тригонометрических функций с помощью чертежа, как это делали недавно. Надо найти косинус того угла, синус которого равен 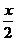 . Подпишем противолежащий катет и гипотенузу,
. Подпишем противолежащий катет и гипотенузу, 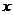 и 2. тогда третья сторона по теореме Пифагора
и 2. тогда третья сторона по теореме Пифагора 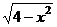 .
.
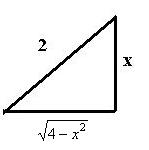
Ну а тогда косинус равен 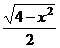 .
.
 =
= 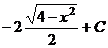 =
= 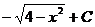 .
.
Примечание. Этот пример можно было решить и другим методом: подведением под знак дифференциала.
ДОК 6 (Л2). Доказать формулу 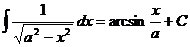
С помощью данной замены докажем эту формулу из таблицы интегралов. Сделаем замену 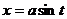 , тогда
, тогда 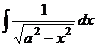 =
= 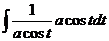 =
= 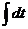 =
= 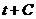 , и обратная замена приводит к
, и обратная замена приводит к 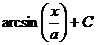 .
.
Случай 2. 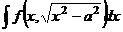 .
.
Здесь замена  (либо аналогично
(либо аналогично 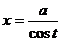 ).
).
Подробнее рассмотрим, как и почему исчезает корень квадратный при замене  . При этом
. При этом 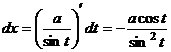 ,
,
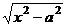 =
=  =
=  =
= 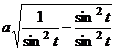 =
= 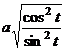 =
= 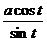 . Таким образом, все корни преобразуются в тригонометрические функции.
. Таким образом, все корни преобразуются в тригонометрические функции.
Случай 3. 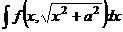 .
.
Замена 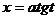 (либо
(либо 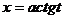 ). Как действует такая замена.
). Как действует такая замена.
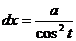 ,
,  =
= 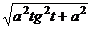 =
= 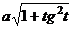 =
= 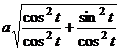 =
= 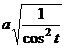 =.
=. 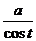 .
.
Итак, корни вида 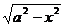 ,
, 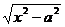 ,
, 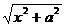 могут быть преобразованы к тригонометрическим функциям с помощью замены.
могут быть преобразованы к тригонометрическим функциям с помощью замены.
Формулировка этих пунктов в билете: ДОК 7 (Л2).
Доказать, что замены сводят интегралы к рациональной дроби.
а) для интеграла 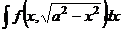 замена
замена 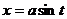
б) для интеграла 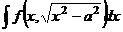 замена
замена 
в) для интеграла 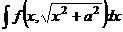 замена
замена 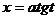
Приложение 1. Вопросы на доказательства (для билетов).
ДОК 1 (Л1).
Докажите формулу интегрирования по частям 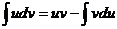 .
.
ДОК 2 (Л1).
Вывести рекуррентную ф-лу 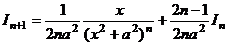
для вычисления интегралов 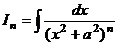 .
.
ДОК 3 (Л2).
Доказать, что интеграл вида 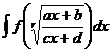 сводятся к рациональной дроби с помощью замены
сводятся к рациональной дроби с помощью замены 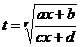 .
.
ДОК 4 (Л2).
Доказать, что при замене 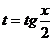 синус и косинус преобразуются по следующим формулам:
синус и косинус преобразуются по следующим формулам: 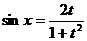 ,
, 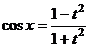 .
.
ДОК 5 (Л2).
Доказать, что если функция нечётна относительно косинуса, замена  сводит интеграл к рациональной дроби, а если
сводит интеграл к рациональной дроби, а если  то замена
то замена  сводит интеграл к рациональной дроби.
сводит интеграл к рациональной дроби.
ДОК 6 (Л2). Доказать формулу 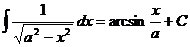
ДОК 7 (Л2).
Доказать, что замены сводят интегралы к рациональной дроби.
а) для интеграла 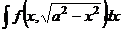 замена
замена 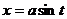
б) для интеграла 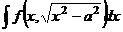 замена
замена 
в) для интеграла 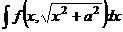 замена
замена 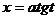
 2018-03-09
2018-03-09 100
100








