Пример 1. Груз массой m (рис. 6.2,а) на пружине жесткости с в вязкой среде, сила сопротивления которой 

Рис.6.2. Колебания: а) - механические с демпфированием подвешенного на пружине груза; б) - амплитудно-частотная характеристика в безразмерных координатах; в)- электрический колебательный контур
На груз действует возмущающая сила 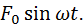 Перемещение груза x является функцией этих величин и времени:
Перемещение груза x является функцией этих величин и времени:
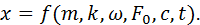 (6.2)
(6.2)
Способ получения критериев следующий. Имеющиеся n величин (в данном случае n=6)  характеризующих процесс, дают n-r критериев подобия
характеризующих процесс, дают n-r критериев подобия
 (6.3)
(6.3)
где r – ранг матрицы,
c – безразмерное число,
pi – размерность i-й величины

Числа 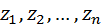 в формуле (3) таковы, что размерность П равна нулю. Поэтому числа
в формуле (3) таковы, что размерность П равна нулю. Поэтому числа  находятся путем решения системы уравнений:
находятся путем решения системы уравнений:

 (6.4)
(6.4)

Система (6.4) имеет n-r независимых решений, в данном случае n=7, r=3? n-r=4. Каждое из решений, состоящее из n значений zi , дает один критерий подобия. Таким образом, предстоит решить систему (6.4). Степени размерностей  для каждой величины указаны в таблице 6.1 (в данном случае
для каждой величины указаны в таблице 6.1 (в данном случае  .
.
Таблица 6.1– Размерности исследуемых величин
| Величина | Степени | |||
| [L] | [M] | [T] | ||
| p1 | m | 
|  1 1
|  0 0
|
| p2 | c |  =0 =0
|  1 1
|  -2 -2
|
| p3 | x |  =1 =1
|  0 0
|  0 0
|
| p4 | t |  =0 =0
|  0 0
|  1 1
|
| p5 | 
|  =1 =1
|  1 1
|  -2 -2
|
| p6 | 
|  =0 =0
|  0 0
|  -1 -1
|
| p7 | k |  =0 =0
|  1 1
|  -1 -1
|
На основании уравнений (6.4) и таблицы 6.1 получаем конкретный вид системы (6.5)
 (6.5)
(6.5)
Как показано ранее, система (6.5) имеет n-r=4 линейно независимых решения. При нахождении этих решений 4 величины Zi, т.е именно 4 независимых решения, имеют в соответствии с требованиями линейной алгебры произвольные значения, остальные три величины находятся из системы уравнений (6.5). Это означает, что четыре величины Zi выбираются произвольно, а остальные три необходимо определять так, чтобы критерий подобия П был безразмерной величиной. Произвол в выборе некоторых чисел Z не имеет значения, важно лишь одно – чтобы величина П была безразмерной. Поэтому нужно выбирать наиболее простые значения, причем, что очень важно, для тех z, для которых это возможно по системе уравнений (6.5). Для данного примера давать одновременно произвольные значения для неизвестных Z1, Z2, Z3 и Z7 - нельзя, т.к. эти переменные входят в первое и второе уравнения системы (6.5) по одному разу и при произвольном выборе этих четырех значений первое и второе уравнения будут взаимно противоречивы. Поэтому принимаем произвольные значения в других сочетаниях переменных. Возможно много вариантов, рассмотрим для примера два из них.
1. Принимаем Z1=1, Z2 = Z6 = Z7=0.
Тогда согласно системе (5) имеем:
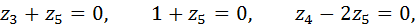
откуда

Итак, первое решение имеет вид:

Аналогичным образом получаем 2-е, 3-е и 4-е решения. приводим их без детальных расчетов:
2. 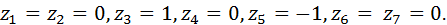
3. 
4. 
Таким образом, получено четыре решения, которым соответствуют четыре независимых критерия подобия.
Из первого решения получаем критерий подобия
 .
.
Из второго решения

Из третьего решения
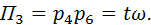
Из четвертого решения

В этом параграфе был продемонстрирован один из методов получения критериев подобия. Критерии подобия можно получить и несколько иным способом. Порядок решения задачи следующий.
Выбираем какие-либо три параметра (по числу первоначальных основных единиц – метр, килограмм, секунда), для которых определитель 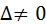 .
.
В соотношении (6.2)  переходим к безразмерным величинам. Такими параметрами могут быть – m,
переходим к безразмерным величинам. Такими параметрами могут быть – m,  .
.
Размерности этих величин выражаются формулами:

Для них
 .
.
Уравнение (2) можно выразить следующим образом:
 . (6.6)
. (6.6)
Значения показателей степени  определяются из условия, что входящие в (6) комплексы – безразмерные величины. Например,
определяются из условия, что входящие в (6) комплексы – безразмерные величины. Например,

Показатели степени при всех размерностях должны равняться нулю, поэтому



теперь получаем выражение для критерия подобия:

Аналогичным образом получены и три другие операторы:
 .
.
Фактически критерии подобия, полученные разными способами – аналогичны. В самом деле  =
=  одна группа независимых величин может быть сведена к другой группе независимых величин, обе группы эквивалентны.
одна группа независимых величин может быть сведена к другой группе независимых величин, обе группы эквивалентны.
Пример 2. Особенно просто критерии подобия находят в том случае, когда имеется дифференциальное уравнение, описывающее поведение системы. Для данного примера дифференциальное уравнение имеет вид:
 (6.7)
(6.7)
Размерности всех членов уравнения (7) одинаковы (правило Фурье), аргумент синуса - безразмерная величина, знак дифференциала на размерность не влияет. Поэтому если, опустив знаки дифференцирования, поделить все члены уравнения на один из его членов, то в результате деления получим безразмерные комплексы величин, т.е критерии подобия. Выполним эту процедуру подробнее.
Уравнение (6.7) в записи без знаков дифференцирования:

Поделим все члены на первый, получим:
 ;
; 
Получившаяся группа из четырех критериев подобия может быть сведена к одной из двух ранее полученных групп.
 2018-03-09
2018-03-09 202
202








