Напряженное и деформированное состояние при растяжении и сжатии

Рассмотрим более подробно особенности напряженного состоя­ния, возникающего в однородном растянутом стержне. Определим напряжения, возникающие на некоторой наклонной площадке, со­ставляющей угол a с плоскостью нормального сечения (рис. 2.3, а).       

Из условия  записанного для отсеченной части стержня (рис. 2.3, б), получим:

где А - площадь поперечного сечения стержня, А _a = А /cos a - пло­щадь наклонного сечения. Из (2.7) легко установить:

Раскладывая напряжение р по нормали и касательной к на­клонной площадке (рис. 2.3, в), с учетом (2.8) получим:

Рис. 2.3

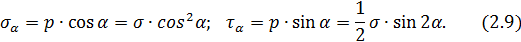
Полученные выражения показывают, что для одной и той же точки тела величины напряжений, возникающих в сечениях, про­ходящих через эту точку, зависят от ориентации этой площадки, т.е. от угла a.При a = 0 из (2.9) следует, что s_a = s, t_a = 0. При a = , т.е. на продольных площадках, s_a = t_a = 0. Это означает, что продольные слои растянутого стержня не взаимодействуют друг с другом. Касательные напряжения t_aпринимают наибольшие зна­чения при a = , и их величина составляет t_max= . Важно отме­тить, как это следует из (2.9), что . Следовательно, в любой точке тела на двух взаимно перпендикулярных площадках касательные напряже­ния равны между собой по абсолютной величине. Это условие является общей закономерностью любого напряженного состояния и носит назва­ние закона парности касательных напряжений.

Теперь перейдем к анализу деформаций в растянутом стержне. Наблюдения показывают, что его удлинение в продольном направ­лении сопровождается пропорциональным уменьшением попереч­ных размеров стержня (рис. 2.4).

Рис. 2.4

Если обозначить:

(2.10)

то, как показывают эксперименты, m = const для данного материала и является безразмерным коэффициентом Пуассона. Вели­чина m является важной характеристикой материала и определяется экспериментально. Для реальных материалов m принимает значе­ния 0,1 ¸ 0,45.

Если мысленно выделить вокруг какой-либо точки тела эле­мент в виде бесконечного малого кубика, то по его граням в об­щем случае будут действовать нормальные и касательные напря­жения (рис. 2.5). Совокупность напряжений на всех элементарных площадках, которые можно провести через какую-либо точку тела, назы­вается напряженным состоянием в данной точке.

Нормальные и касательные напря­жения принято обозначать системой ин­дексов. Нормальное напряжение имеет один индекс, соответствующий той оси, вдоль которой оно направлено. Касательным напряжениям присваивают два индекса: первый индекс указывает, относительно какой оси параллельна нормаль к площадке действия рассматриваемого напряже­ния, второй — какой оси — это напряжение параллельно.

 Рассмотрим вопросы, связанные с анализом напряженного состояния.

В каждой исследуемой точке напряженного тела существует такая система осей х, у, z, для которой касательные напряжения равны нулю. Такие оси называются главными осями, соответ­ствующие им взаимно перпендикулярные площадки — главными площадками, а нормальные напряжения на них — главными напряжениями. В порядке возрастания эти напряжения обознача­ются через σ₁, σ₂ и σ₃,. Таким образом, σ₁ > σ₂> σ₃.

Если все главные напряжения отличны от нуля, то напряжен­ное состояние называется трехосным или объемным (рис. 2,6,а).

Рис. 2.6

Если равно нулю одно из главных напряжений, то напряженное состояние называется двухосным или плоским (рис. 2.6, б). Если равны нулю два главных напряжения, то напряженное состояние называется одноосным или линейным (рис. 2.6, в).