Обобщенный закон Гука

Определим деформации ε₁, ε₂ и ε₃ в направлениях главных на­пряжений для трехосного напряженного состояния. Для этого используем закон Гука для одноосного напряженного состоя­ния, зависимость между продольной и поперечной деформация­ми и принцип независимости действия сил (принцип сложения деформаций).

Относительное удлинение в направлении главного напряже­ния σ₁ складывается из составляющей σ₁/E, обусловленной дей­ствием главного напряжения σ₁, и составляющих 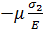, , 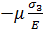обусловленных действием главных напряжений σ₂ и σ₃. Следовательно,

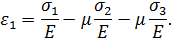
Такие же выражения получаются для ε₂ и ε₃. В итоге имеем:

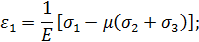
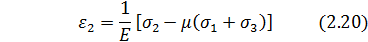
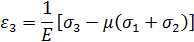
Уравнения (2.18) представляют собой обобщенный закон Гука для объемного напряженного состояния. Деформации ε₁, ε₂ и ε₃ в направлениях главных напряжений называются главными де­формациями. Для плоского напряженного состояния (σ₃ = 0) оп­ределение главных напряжений σ₁, и σ₂ по известным главным деформациям ε₁ и ε₂ производится по формулам

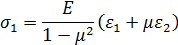
                                                                     (2.21)

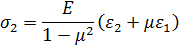
С учетомε₁, ε₂ и ε₃ можно вычислить изменение объема при деформации кубика размером 1x1x1 и объемом V₀ = 1. После деформации его объем

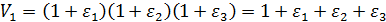
(произведениями ε как величинами малыми по сравнению с са­мими ε пренебрегаем).

Относительное изменение объема, как объемная деформация,

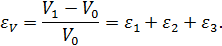
Подставив значения ε₁, ε₂ и ε₃ из уравнений (3.7), получим

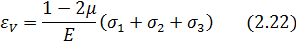
Из формулы (2.22) следует, что коэффициент Пуассона μ не может быть больше 0,5, поскольку при трехосном растяжении, очевидно, объем элемента не способен уменьшиться. При μ = 0,5 ε_V= 0, т. е. объем элемента при деформации не изменяется.

 

Лекция №3.

3. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ СЕЧЕНИЙ.

Известно, что сила, которую может выдержать стержень на растяжение, пропорциональна площади поперечного сечения. Однако, площадь поперечного сечения не является исчерпывающей характеристикой. Сечения разной конфигурации могут иметь одинаковую площадь, но их поведение при различных способах нагружения будет различным. Простейший пример: полоса металла или бумаги, будучи согнутой (угловое сечение) приобретает способность сопротивляться изгибу в гораздо большей мере, чем такая же плоская полоса.

Для того, чтобы охарактеризовать геометрические свойства поперечных сечений стержней при различных способах нагружения, необходимо ввести более сложные характеристики – моменты площадей.

3.1. Некоторые сведения о геометрических характеристиках

Геометрические характеристики - числовые величины (параметры), определяющие размеры, форму, расположение поперечного сечения однородного по упругим свойствам деформируемого элемента конструкции (и, как след­ствие, характеризующие сопротивление элемента различным видам дефор­мации).

Рассмотрим произвольное поперечное сечение А (сечение бруса) (рис. 3.1) с координатами центра тяжести x _c, у_c. В точке (x, у) выделим элемент площади dA. Основные геометрические характеристики попе­речных сечений элементов конструкций описываются интегра­лами следующего вида

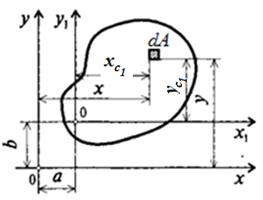
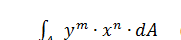
Рассмотрим некоторые характерные варианты записи этого интеграла и получим выраже­ния для основных геометрических характеристик.

Площадь поперечного сечения

При т=0,n=0 интеграл приобретает вид

 

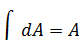
а соответствующая характеристика, как видим, представляет собой площадь поперечного сечения элемента.

Как было указано во многих случаях деформирования тела знание только площади его по­перечного сечения недостаточно.

3.2. Статические моменты

Статический момент относительно данной оси - сумма произведений эле­ментарных площадей dAна их расстояние до данной оси, взятая по всей площади сечения А.

Если в уравнении 3.1 т=1, n=0, тогда получим статическим моментом относительно оси x

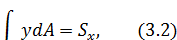
прит=0, п=1, получим выражение для статическим моментомотносительно оси у.

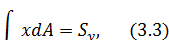
Для сложного сечения (состоящего из нескольких простых, каждое из кото­рых имеет площадь А_i и координаты собственного центра тяжести )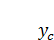

 

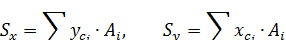
Отсюда можем получить формулы для определения координат центра тяже­сти сечения:                                                                      

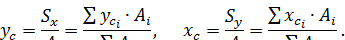
Статические моменты в этом случае равны нулю, а сами оси называются центральными. Размерность статических моментов в системе СИ – м³.

При выполнении практических расчетов важно знать, как ме­няются статические моменты сечения при параллельном переносе координатных осей (рис 3.1).

В соответствии с рисунком 3.1, очевидно, что

х = х₁ + а у = у₁ + b. (3.3)

Подставляя (3.1) и (3.2) в (3.3) получим:

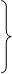
                                                                           (3.4)

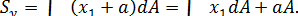
Величины a и b в уравнении 3.4можно подобрать так, чтобы выполнялись следующие равенства (причем единственным обра­зом):

b∙A=S_x, a∙A=S_y, (3.5)

В этом случае статические моменты относительно осей будут равны = 0.

Точка С(х_с,y_c) пересечения централь­ных осей называется центром тяжести сечения в системе координат (х, у)и определяется из (3.5):

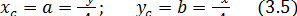
Если предположить, что брус имеет составное сечение с общей площадьюA. Обозначим черезA_k (k = 1,2,3,...,n) площадь k- ой области, принадлежащей к составному сечению бруса. Тогда выражение (3.1, 3.2) можно преобразовать в следующем виде:

 

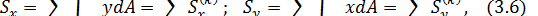
где - статические моменты k-той области относительно осей х и у., следовательно, статический момент составного сечения равен сумме статических моментов составляющих областей.

 

3.3. Моменты инерции сечения

Для оценки напряженного состояния нагружаемых элементов применяют еще три момента второго порядка

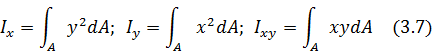
Первые две величины называют осевыми моментами инерции относительно осей x и y, а 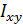- центробежным моментом инерции.

Кроме осевого и центрального момента инерции используется еще один интеграл 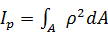, который называется полярным моментом инерции. Очевидно, что 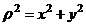, и:

,

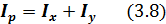Осевой момент инерции относительно данной оси — сумма произведений элементарныx площадей dAна квадрат их расстояний до данной оси, взятая по всей площади сечения А.

Если в уравнении 3.1 т = 2, n = 0, получаем, что осевым моментом инерции относительно оси x равен:

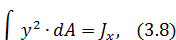
прит=0, n=2,                               

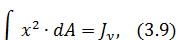
осевым моментом инерции относительно оси у.