2018-03-09
135
Вариант 10
1. Решить системы уравнений методом Крамера:
а) 
в) 
б) 
г) 
2. Решить системы уравнений методом Гаусса:
а) 
б) 
3. Решить систему уравнений двумя методами:
Практическая работа №4
Тема: Вычисление пределов функций
Цель: научиться вычислять пределы функций по определению, с использованием замечательных пределов.
Методические указания по выполнению практической работы
1. Повторите основные определения и теоремы о пределах
2. Разберите примеры применения теорем и формул
3. Подберите для каждого задания соответствующие формулы и правила
Определение 1. Число b называют пределом функции f(x), если в любой заранее выбранной окрестности точки b содержатся все значения функции, начиная с некоторого значения.
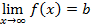
(читают: предел функции y=f(x) при стремлении x к бесконечности равен b)
Теоремы о пределах
Пример 1. Вычислить: 
Решение: разделим числитель и знаменатель дроби почленно на 
:
Предел функции в точке
Пример 2. Вычислить:
а) выражение 
определено в любой точке x, поэтому предел функции при стремлении x к 1 равен значению функции в точке x=1:
б) выражение 
определено в любой точке x≥0, следовательно, предел функции при стремлении x к 2 равен значению функции в точке x=2:
в) если подставить значение x=-3 в заданное выражение, то и в числителе, и в знаменателе получится 0, а на 0 делить нельзя. Но заданную алгебраическую дробь можно сократить:
Замечательные пределы
Первый замечательный предел
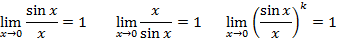
Основные тригонометрические тождества: 
Формулы двойного угла: 
Формулы половинного аргумента: 
Пример 3. Вычислить: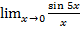 
Решение:
Второй замечательный предел
Пример 4. Вычислить: 
Решение:
Вопросы для самоконтроля:
1. Дайте определение бесконечно малой величины (БМВ). Приведите примеры.
2. Какую величину называют бесконечно большой (ББВ)?
3. Какая связь существует между БМВ и ББВ?
4. Перечислите теоремы о пределах и следствия из них.
5. Что представляет собой число е?
Задания к практической работе
Вариант 10
Вычислить пределы функций:
