Методические указания по выполнению практической работы

1. Повторите основные определения; формулы и правила вычисления производной

2. Повторите геометрический и физический смысл производной; разберите примеры 1, 2

3. Выполните задания №№ 1, 2

4. Проработайте алгоритмы применения производной; разберите примеры

5. Выполните задания №№ 3 – 6

 

Геометрический смысл производной

Касательной к данной кривой в данной точке называется предельное положение секущей.

Прямая, проходящая через данную точку перпендикулярно касательной, называется нормалью к кривой в данной точке.

y=f(x)

нормаль

касательная

α

x

y

                                                                                 

                                                                                        

 

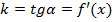                                                     угловой коэффициент касательной

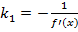 угловой коэффициент нормали

Физический смысл производной

С физической точки зрения мгновенная скорость – это производная от пути: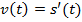

Пример1. Найти угловой коэффициент касательной и нормали к графику функции 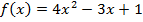 в точке с абсциссой .

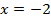Решение. Найдем производную функции: .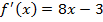

.

.

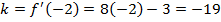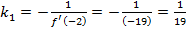Физический смысл второй производной

Ускорение 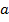 прямолинейного движения точки в данный момент времени равно второй производной пути по времени:

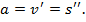
Пример 2. Точка движется прямолинейно по закону 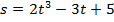. Вычислить скорость и ускорение точки в момент времени .

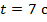Решение.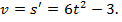

При 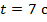 скорость равна: .

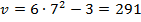Ускорение 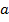 равно:

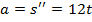
При 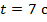 ускорение равно: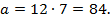

Исследование функций с помощью производных

Возрастание и убывание функций

Возрастание и убывание функции 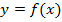характеризуется знаком ее производной: если на некотором промежутке 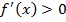, то функция на этом промежутке возрастает; если же 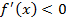, то функция на этом промежутке убывает.

Пример 3. Найти промежутки возрастания и убывания функции

                   .

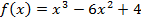Решение.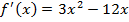

f’(x)     +            -           +                    0          4

,

.

 

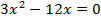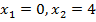Ответ. На промежутках 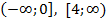функция возрастает, на промежутке  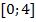функция убывает.

Алгоритм исследования функции на максимум и минимум с помощью первой производной

1. Найти производную .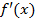

2. Найти критические точки функции, т.е. точки, в которых 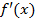обращается в нуль или терпит разрыв.

3. Исследовать знак производной в промежутках, на которые найденные критические точки делят область определения функции. Если при переходе через критическую точку 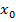 производная меняет знак с положительного на отрицательный, то  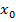– точка максимума. Если с отрицательного на положительный, то  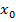– точка минимума.

4. Вычислить значения функции в точках максимума и минимума.

Пример 4. Исследовать функцию на экстремум: .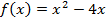

f’(x)    -           +                     2

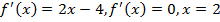Решение.  – критическая точка.

 

 

Получаем,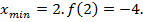

 

Алгоритм исследования функции на экстремум с помощью второй производной

1. Найти производную функции .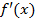

2. Найти критические точки данной функции, в которых .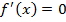

3. Найти вторую производную .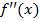

4. Исследовать знак второй производной в каждой из критических точек. Если при этом вторая производная окажется отрицательной, то функция в такой точке имеет максимум, а если положительной, то – минимум. Если вторая производная окажется равной нулю, то исследование нужно провести с помощью первой производной.

5. Вычислить значения функции в точках максимума и минимума.

Пример 5. Исследовать функцию на экстремум с помощью второй производной: .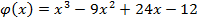

Решение. 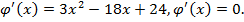Получим критические точки . .

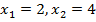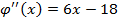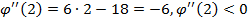, т.е.  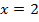– точка максимума.

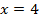, т.е.  – точка минимума.

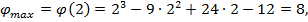
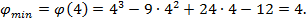
Функция имеет максимум в точке (2;8), минимум в точке (4;4).

 

Направление выпуклости графика

Определение 1. Кривая 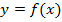называется выпуклой вниз в промежутке, если она лежит выше касательной к кривой, проведенной в любой точке этого промежутка.

Определение 2. Кривая 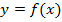называется выпуклой вверх в промежутке, если она лежит ниже касательной к кривой, проведенной в любой точке этого промежутка.

y=f(x)

a           b  x

y

y=f(x)

y

a             b      x

 

 

Если в некотором промежутке 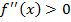, то кривая выпукла вниз в этом промежутке; если же 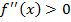, то кривая выпукла вверх в этом промежутке.

Пример 6. Найти промежутки выпуклости кривой .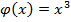

Решение. 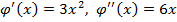.  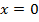– критическая точка.

В промежутке 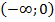 имеем 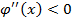, значит на этом промежутке кривая выпукла вверх. В промежутке  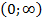имеем 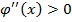, значит на этом промежутке кривая выпукла вниз.

 

Точки перегиба

Определение 3. Точка графика функции 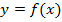, разделяющая промежутки выпуклости противоположных направлений этого графика, называется точкой перегиба.

Правило нахождения точек перегиба графика функции

1. Найти вторую производную .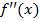

2. Найти критические точки функции, в которых 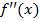обращается в нуль или терпит разрыв.

3. Исследовать знак второй производной 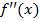в промежутках, на которые найденные критические точки делят область определения функции. Если при этом критическая точка  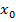разделяет промежутки выпуклости противоположных направлений, то  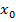является точкой перегиба функции.

4. Вычислить значения функции в точках перегиба.

 

Пример 7. Найти точку перегиба кривой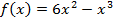

Решение. .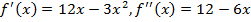

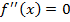, получим критическую точку .

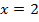В промежутке 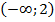 имеем 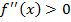, а в промежутке  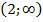имеем 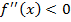. Значит,  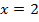точка перегиба.

 

Вопросы для самоконтроля:

1. Какая связь существует между непрерывностью функции и ее производной?

2. Объясните геометрический смысл производной.

3. Запишите уравнение касательной и нормали, проведенных через данную точку кривой.

4. Какие физические задачи решаются с применением производной?

5. Укажите признаки существования максимума и минимума функции.

6. Как находится наименьшее и наибольшее значения функции на отрезке?

7. Как исследуется функция на точки перегиба с помощью второй производной?