Тема: Вычисление производных первого и второго порядка
Цель: научиться применять формулы и правила дифференцирования для вычисления производных первого и второго порядка
Методические указания по выполнению практической работы
1. Повторите основные определения; формулы и правила вычисления производной
2. Разберите примеры 2, 3
3. Выполните задания
Определение 1. Производной функции 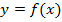 называется предел отношения приращения функции
называется предел отношения приращения функции 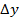 к приращению аргумента
к приращению аргумента 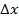 при
при 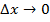 :
:
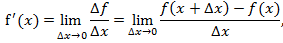
если этот предел существует.
Производная функции имеет следующие обозначения: 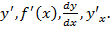
Процесс вычисления производной называется дифференцированием.
Формулы дифференцирования
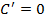
| 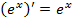
|
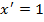
| 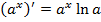
|
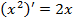
| 
|
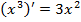
| 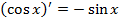
|
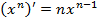
| 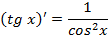
|
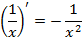
| 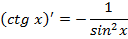
|
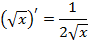
| 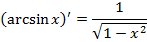
|
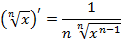
| 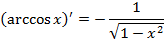
|
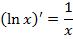
| 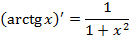
|
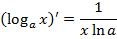
| 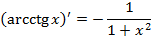
|
Правила дифференцирования
1. 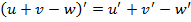
2. 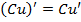
3. 
4. 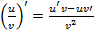
5. 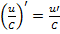
6. 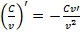
Производная сложной функции
Определение 2. Функция вида 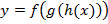 называется сложной функцией.
называется сложной функцией.
Производная сложной функции вычисляется по формуле:

Производная второго порядка
Определение 3. Если существует производная от производной 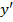 функции
функции 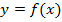 , то она называется второй производной или производной второго порядка, т. е.
, то она называется второй производной или производной второго порядка, т. е.
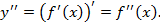
Пример 3. Найти вторую производную функции 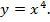
Решение. Находим первую производную: 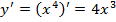 . Полагая первую производную функцией, вычисляем вторую производную:
. Полагая первую производную функцией, вычисляем вторую производную:
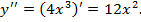
Вопросы для самоконтроля:
1. Дайте определение производной функции.
2. Сформулируйте правила нахождения производной функции.
3. Как вычисляется производная сложной функции?
4. Что называется производной второго порядка?
Задания к практической работе
Вариант 10
1. Найдите производную функции:
а) 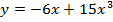 в)
в) 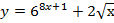
б) 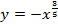 г)
г) 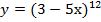
2. Вычислите производную функции при данном значении аргумента:
а) 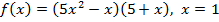
| в) 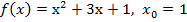
|
б) 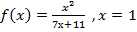
| г) 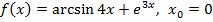
|
3. Найдите вторую производную функции:
а) 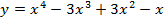
| в) 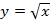
|
б) 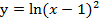
| г) 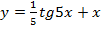
|
4. Решите уравнение: 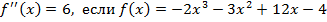
Практическая работа №6
Тема: Применение производных
Цель: научиться применять производную для исследования функций, решения задач геометрического и физического содержания.
 2018-03-09
2018-03-09 352
352








