2018-03-09
186
Статистические показатели являются результатом измерения общественных явлений. Статистический показатель – это число, характеризующее ту или иную особенность явлений.
Различают индивидуальные и обобщающие статистические показатели. Использование индивидуальных показателей отдельных аграрных образований и позволяет выявить передовые тенденции их развития. Обобщающие статистические показатели подразделяются на две большие группы: экстенсивные (объемные) и интенсивные (качественные) показатели. Экстенсивные показатели исчисляются по первичным признакам, а интенсивные – по вторичным.
Экстенсивные (объемные) статистические показатели характеризуют объем, массу общественных явлений, они получаются как итог непосредственного подсчета или суммирования статистических данных (индивидуальных показателей или отдельных их составляющих).
Экстенсивные показатели могут определять: а) численность единиц совокупности (например, подсчет численности работников); б) объем (итог) значений признака по совокупности (допустим, подсчет фонда заработной платы работников организаций).
|
|
|
Интенсивные (качественные) показатели рассчитываются на единицу совокупности, что позволяет улавливать типические тенденции в развитии явлений и сохранить большую устойчивость в пространстве и времени. Интенсивные обобщающие показатели подразделяются на: средние показатели (средняя заработная плата, средняя себестоимость единицы продукции и т.д.) и относительные величины (темпы роста и прироста, индексы, удельные веса и др.).
Средние величины – это показатели, выражающие типичные черты явления и дающие обобщающую количественную характеристику уровня по однородным явлениям. Основным условием правильного использования средней является качественная однородность совокупности, по которой исчисляется средняя величина. При изучении явлений в аграрной экономике наиболее часто используются средняя арифметическая простая и взвешенные величины.
Если исходные данные осредняемого признака представлены в несгруппированном виде (как индивидуальные значения признака у отдельных единиц совокупности), то в этом случае средняя рассчитывается по формуле средней арифметической простой:
,
где 
– среднее значение признака;
x – индивидуальное значение признака у каждой единицы совокупности;
å – знак суммирования,
n – число единиц совокупности.
Если данные представлены в сгруппированном виде, т.е. в виде рядов распределения (дискретных или интервальных), то средняя в таких случаях рассчитывается по формуле средней арифметической взвешенной:
|
|
|
,
где x – варианты значений осредняемого признака;
f – частоты (веса) для каждого из вариантов признака, показывающие их повторяемость.
Частоты ряда распределения можно заменить их удельными весами, т.е.:
.
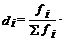
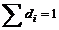В таком случае формула расчета средней примет вид
.
Если известны варианты значений осредняемого признака (х) и их итоговые результаты (М), то в этом случае средняя рассчитывается по формуле средней гармонической взвешенной
,
где M = xf.
При М – const средняя гармоническая взвешенная преобразуется в среднюю гармоническую простую
.
Определим среднюю продуктивность коров (табл. 7.1):
Т а б л и ц а 7.1. Исходные данные
| Номер сельхозорганизации | Продуктивность коров, ц (Х) | Поголовье, гол. (f) | Доля (d) | Валовый надой молока, ц (М) |
| 1 2 3 | 30 36 42 | 200 300 500 | 0,2 0,3 0,5 | 6000 10800 21000 |
| И т о г о… | 37,8 | 1000 | 1,00 | 37800 |
ц.
Такой же результат получим, используя формулу
= 30∙0,2+36∙0,3+42∙0,5 = 37,8 ц.
Вычислим среднюю продуктивность коров, используя среднюю гармоническую
Сочетание средних и индивидуальных величин при характеристике изучаемой совокупности является необходимым приемом осуществления группировок.
Абсолютные величины – это количественные показатели, которые выражают объемы, размеры, уровни социально-экономических явлений.
Важнейшими из качественных показателей являются относительные величины, посредством которых дается оценка сравнимых исследуемых явлений, их качественные особенности.
Относительная величина – это мера соотношения объема признака или совокупности с базой. Объемы признака или совокупности могут сравниваться с другими их состояниями (во времени, в пространстве или установленными заданиями) или со значениями других взаимосвязанных признаков (сравнение значений разноименных признаков), могут также сравниваться части признака или объема совокупности с их общими объемами (сравнение части и целого).
Относительная величина всегда представляет собой отношение двух величин (преимущественно абсолютных). По своему содержанию относительные величины могут быть подразделены на несколько видов. Основными из них являются относительные величины динамики, выполнения установленного задания (плана) и планового (установленного) задания, пространственного сравнения, координации, интенсивности, структуры.
2. Графический прием позволяет посредством геометрических образов (точек, линий, фигур, их сочетания) отобразить взаимосвязь между явлениями, основные тенденции их развития, степень распространенности и т.д. Основными видами графиков являются диаграммы (линейные, столбиковые, секторные, круговые), планово-линейные графики (применяются для контроля за ходом выполнения задания и строятся на разграфленной сетке, данные о выполнении плана наносятся на график в процентах), картограммы (географические карты или схемы), специальные графики (они отражают взаимосвязь явлений; к ним, например, относится поле корреляции).
Схема – это изображение, передающее обычно с помощью условных обозначений и без соблюдения масштаба основную идею какого-либо устройства, сооружения или процесса и показывает взаимосвязь их главных элементов.
В экономических работах часто используются блок-схемы, в которых составляющие элементы изображаются в виде прямоугольников с простыми связями в виде линий.
Диаграмма – один из способов графического изображения зависимости между величинами. Диаграммы составляются для наглядного изображения и используются при анализе значительного объема данных, особенно в статистике и экономике. Выбор диаграммы зависит от тех задач, для решения которых она предназначена. Она может быть плоскостной, линейной и объемной. Ее следует создавать с использованием табличного процессора MicrosoftExcel, который предлагает 14 различных стандартных типов диаграмм с выделением подтипов: гистограмма, линейчатая, график, круговая, точечная, с областями, кольцевая, лепестковая, поверхность, пузырьковая, биржевая, цилиндрическая, коническая, пирамидальная.
|
|
|
В курсовых, дипломных работах наибольшее распространение получили линейные диаграммы, а из плоскостных – столбиковые (ленточные) и секторные.
Для линейных диаграмм применяют координатное поле. По оси абсцисс в масштабе откладывается время или фактические признаки (независимые друг от друга), а на оси ординат – показатели на определенный момент или период времени. На оси ординат может быть размещена и величина как в количественных, так и в относительных цифрах, характеризующих этот независимый признак. Вершины ординат на таких диаграммах соединяются отрезками, что позволяет получить ломаную линию. На линейные диаграммы одновременно может быть нанесено значительное число показателей, что позволяет убедительно и наиболее просто проводить их сопоставительный анализ для формулирования соответствующих выводов или положений.
На столбиковых диаграммах данные изображаются в виде прямоугольников (столбиков) одинаковой ширины, размещенных вертикально или горизонтально. Длина (высота) прямоугольников должна быть пропорциональна величинам изучаемого объекта или явления.
На секторных диаграммах показывает как абсолютную величину каждого элемента ряда данных, так и его вклад в общую сумму. Такую диаграмму целесообразно использовать, когда необходимо подчеркнуть значение какого-либо элемента. На ней лучше всего видно, какую часть целого составляет тот или иной компонент.
3. Прием экономического сравнения используется для выявления различий и сходства в развитии изучаемых явлений в выделенных группах. Важной разновидностью данного приема является сравнение по периодам. Его применяют при наличии данных за многие годы. Но данный прием можно использовать только при сопоставимости статистических данных по изучаемым признакам. Так, например, нецелесообразно сравнивать стоимостные показатели за 1980–1990 гг. и 1991–2002 гг. в связи с произошедшими переменами в экономике.
|
|
|
4. Прием сопоставления параллельных рядов, т.е. сравнения совокупности показателей, обладающих свойством сопоставимости, используется для выявления характера изучаемых явлений. Например, сравнение показателей, характеризующих развитие скотоводства, в анализируемой и передовой организации.
5. Индексный анализ производится с помощью расчета индексов. Индекс – это относительный статистический показатель, характеризующий соотношение во времени (динамический индекс) или в пространстве (территориальный индекс) уровней экономических явлений. Различают индексы индивидуальные и общие. Индивидуальный индекс динамики явлений исчисляется как отношение индивидуального уровня явления отчетного периода (например, цены товара исследуемой ассортиментной группы – 
к индивидуальному уровню явления базисного периода 
, т. е., 
. Подобным способом исчисляется и индивидуальный индекс физического объема 
и другие индексы. Общие индексы характеризуют динамику сложных экономических явлений в среднем. Так, наблюдается рост цен по исследуемым товарам (индекс цен 
). Возрос и объем продажи этих товаров (индекс физического объема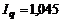 
).
Агрегатные индексы являются основной формой общих индексов. На их основе раскрываются конкретные взаимосвязи экономических явлений. Они позволяют определить роль влияния каждого из факторов на динамику результативного (интегрального показателя).
Связь между индексами выражается теми же соотношениями, как и связь между признаками: произведение агрегатного индекса цен 
на агрегатный индекс физического объема 
равно агрегатному индексу товарооборота 
, т. е.
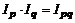
, или
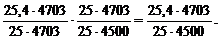
Вычитая из числителя каждого агрегатного индекса его знаменатель, можно получить величины абсолютных приростов: общего изменения товарооборота 
– 
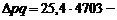тыс. рублей) прироста товарооборота за счет изменения уровней цен 
тыс. рублей) и прироста товарооборота за счет изменения физического объема продукции 
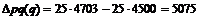тыс. рублей).
6. Прием экономической группировки, под которым понимают деление совокупности данных на группы по определенным, наиболее существенным признакам с последующей характеристикой этих групп с помощью обобщающих показателей.
7. Прием косвенного использования группировок.
8. Когда невозможно собрать массовый материал по изучаемому вопросу, то для количественной характеристики зависимости явлений используют дисперсионный анализ (т.е. на базе изучаемой совокупности определяют общую 
, факторную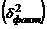 
и остаточную 
дисперсию, определяют их удельный вес (доли каждой дисперсии в общей), производят корректировку дисперсии на число степеней свободы, определяют коэффициент Фишера, делают выводы.
Так, общую дисперсию разлагают на составляющие
,
где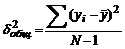 
;
;
;
где 
– расчетное значение результативного признака;
– фактическое значение результативного признака;
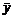– среднее значение результативного признака;
N – количество опытов (повторностей);
m – количество признаков, включая результативный.
Отношение факторной дисперсии 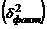к общей дает коэффициент детерминации (D), который характеризует долю вариации результативного признака, обусловленного вариацией исследуемых факторных признаков.
9. Корреляционно-регрессионный анализ проводится на базе использования массовых данных и позволяет составить уравнение регрессии, из которого можно получить количественную оценку влияния факторных признаков на результат.
