Формулу Эйлера для определения критической силы при различных закреплениях концов стержня можно записать как  .
.
Коэффициент  позволяет любой случай закрепления концов стержня свести к основному случаю – к стержню с шарнирно закрепленными концами.
позволяет любой случай закрепления концов стержня свести к основному случаю – к стержню с шарнирно закрепленными концами.
Для шарнирно закрепленных концов  ;
;
Для стержня с закрепленными концами  ;
;
Для стержня с одним закрепленным и другим свободным концом  ;
;
Для стержня с одним заделанным и другим шарнирно закрепленным концом 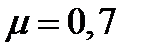 .
.
По какой формуле вычисляется критическое напряжение?
Критическое сжимающее напряжение, т.е. такое, при котором прямолинейная форма равновесия стержня становится неустойчивой, определится по формуле
 .
.
Введем понятие гибкости стержня 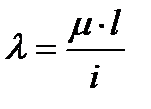 , получим
, получим  , где
, где  - радиус инерции поперечного сечения стержня.
- радиус инерции поперечного сечения стержня.
Что понимается под гибкостью стержня?
Безразмерная величина  носит название гибкости стержня и характеризует его способность сопротивляться искривлению в зависимости от размеров и способа закрепления концов.
носит название гибкости стержня и характеризует его способность сопротивляться искривлению в зависимости от размеров и способа закрепления концов.
Предельная гибкость  , при которой формула Эйлера еще применима. Например, для стали Ст3
, при которой формула Эйлера еще применима. Например, для стали Ст3  , при
, при  нужно пользоваться формулой Ясинского.
нужно пользоваться формулой Ясинского.
Определить область применимости формулы Эйлера при расчетах на устойчивость.
Приведенная формула Эйлера справедлива тогда, когда напряжение  в материале, вызванное критической силой, не превышает предела пропорциональности, т.е.
в материале, вызванное критической силой, не превышает предела пропорциональности, т.е.  . Формулой Эйлера можно пользоваться лишь в пределах применимости закона Гука
. Формулой Эйлера можно пользоваться лишь в пределах применимости закона Гука
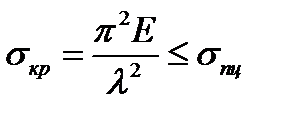 .
.
Отсюда получим формулу для предельной гибкости  .
.
Условие применимости формулы Эйлера можно представить в виде  .
.
 2018-03-09
2018-03-09 227
227








