Как определяются напряжения при внецентренном растяжении (сжатии) ?

Если на жесткий брус в его верхнем поперечном сечении одновременно действуют продольная сила  и изгибающие моменты  и , то нормальное напряжение в произвольной точке равно сумме напряжений

.

Формулу можно использовать, если сила  приложена не по центру, а, например, в точке со смещением и .

Как определяются напряжения при косом изгибе?

Косой изгиб можно рассматривать как сочетание двух прямых изгибов, вызванных изгибающими моментами относительно главных центральных осей инерции поперечного сечения.

Напряжение в любой точке определяется как .

Как определяется приведенный (эквивалентный) момент по третьей и четвертой теориям прочности?

По третьей теории прочности .

По четвертой теории прочности , где 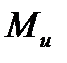- изгибающий момент, - крутящий момент.

По какой формуле можно определить предварительный диаметр вала, работающего на кручение?

Валы обычного работают на кручение с изгибом. Предварительный диаметр вала с учетом только кручения определяют из условия прочности по заниженным допускаемым напряжениям

после этого разрабатывают схему нагружения вала и уточняют диаметр вала по приведенному моменту.

 

Как определяются напряжения по третьей и четвертой теориям прочности при изгибе с кручением?

По третьей теории прочности .

По четвертой теории прочности .

Соответственно условия прочности имеют вид:

 , .