Метод элементарных преобразований

Ранг матрицы равен числу ненулевых строк в матрице после приведения её к ступенчатой форме при помощи элементарных преобразований над строками матрицы.

Метод окаймляющих миноров

Пусть в матрице найден ненулевой минор -го порядка . Рассмотрим все миноры -го порядка, включающие в себя (окаймляющие) минор ; если все они равны нулю, то ранг матрицы равен . В противном случае среди окаймляющих миноров найдется ненулевой, и вся процедура повторяется.

 

Пространство арифметических векторов. Критерий линейной зависимости системы арифметических векторов. Теорема о базисном миноре. Критерий линейной зависимости строк (столбцов) квадратной матрицы.

Арифметическим вектором называется упорядоченная совокупность n чисел.

Обозначается x = (x ₁, x ₂,..., x _n);

числа x ₁, x ₂, ...,x_n называются компонентами арифметического вектора.

Для арифметических векторов определены линейные операции — сложение арифметических векторов и умножение вектора на число:

для любых x = (x ₁, x ₂,..., x _n), y = (y ₁, y ₂,..., y _n) и любого числа α справедливо:

x + y = (x ₁+ y ₁, x ₂ + y ₂,..., x _n + y_n);α x = (αx ₁, αx ₂,..., α x _n).

Множество арифметических векторов, для которых определены операции сложения и умножения на число называется пространством арифметических векторов Rn.

Вектор θ = (0, 0,..., 0) называется нулевым вектором Rn,

а вектор − x = (−x ₁, −x ₂,..., −x _n) — противоположным вектором для вектора x в Rn.

 

Линейной комбинацией векторов e₁,e₂,..., e_k линейного пространства L называется выражение С₁·e₁+С₂·e₂+...+С_k· e_k. Числа С₁, С₂,..., С_k — коэффициенты линейной комбинации

Если все коэффициенты линейной комбинации С₁·e₁+С₂·e₂+...+С_k· e_k равны нулю, то она называется тривиальной линейной комбинацией.

Система e ₁, e ₂,..., e _k линейно независима, если равенство С₁· e ₁+С₂ ·e ₂+...+С_k · e _k = 0 возможно только для тривиальной линейной комбинации.

Система e₁,e₂,..., e_k линейно зависима, если существует нетривиальная линейная комбинация, для которой справедливо равенство С₁·e₁+С₂·e₂+...+С_k· e_k = 0.

 

Для того, чтобы система векторов линейного пространства была линейно зависма, необходимо и достаточно, чтобы хотя бы один из векторов системы линейно выражался через остальные векторы системы (мог быть представлен в виде разложения по векторам системы).

 

Система векторов линейного пространства L образует базис в L если эта система векторов упорядочена, линейно независима и любой вектор из L линейно выражается через векторы системы.

Иными словами, линейно независимая упорядоченная система векторов e₁,..., e _n
образует базис в L если любой вектор x из L может быть представлен в виде

x = С₁·e₁+С₂·e₂+...+С _n · e _n.

 

Можно определить базис иначе.

Любая упорядоченная линейно независимая система e₁,..., e _n векторов n- мерного линейного пространства L_n образует базис этого пространства.

Поскольку n, размерность пространства L_n — максимальное количество линейно независимых векторов пространства, то система векторов x,e₁,..., e _n линейно зависима и, следовательно, вектор x линейно выражается через векторы e₁,..., e _n:

x = x ₁·e₁+ x ₂·e₂+...+ x_n · e _n.

Такое разложение вектора по базису единственно.

 

(Теорема о базисном миноре). Базисные строки и столбцы линейно независимы. Любая другая строка или столбец матрицы являются линейной комбинацией базисных строк или столбцов.

Доказательство проведем для строк. Покажем вначале, что базисные строки линейно независимы. Если бы они были линейно зависимы, то одна из этих строк была бы линейной комбинацией остальных. Тогда на основании свойств определителя эту комбинацию можно вычесть из указанной строки и получить на ее месте ноли. Но если вся строка состоит из нолей, то минор равен нулю, что противоречит теореме.

Докажем вторую часть этой теоремы. Рассмотрим любой минор -го порядка, включающий в себя базисный. Расположим базисный минор в левом верхнем углу:

.

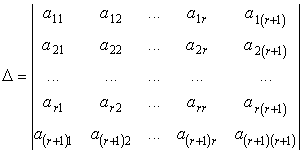По определению данный минор равен нулю. Раскроем его по последнему столбцу:

.

Здесь , разделим на него все равенство:

Из полученного выражения следует, что -ая строка является линейной комбинацией базисных строк.

Отсюда можно сделать вывод, что число линейно независимых строк или столбцов равно рангу матрицы. Это свойство используется для практического вычисления .