Если  - частные решения СЛАУ AX=B,
- частные решения СЛАУ AX=B,
Z1, …, Zn-z - ф.с.р. приведенной СЛАУ AX=0,
то  +c1Z1+c2Z2+…+cn-zZn-z - общее решение СЛАУ AX=B.
+c1Z1+c2Z2+…+cn-zZn-z - общее решение СЛАУ AX=B.
12. Геометрическое векторное пространство:
В инженерной графике геометрическое пространство рассматривается как множество однородных элементов. К основным формообразующим элементам геометрического пространства относятся точки, линии (прямые и кривые), поверхности (плоские и кривые).
Различают пространство евклидово и неевклидово. Евклидово пространство характеризуется тем, что расположенные в нем параллельные прямые линии или плоскости не пересекаются. Соотвественно Неевклидово наоборот.
Базис в пространстве, на плоскости и на прямой.
Базисом векторного пространства называется
На прямой 1) любой ненулевой вектор коллинеарный прямой
На плоскости 2)любая упорядоченная пара неколлинеарных векторов пространства
В пространстве 3)любая упорядоченная тройка некомпланарных векторов (т.е. не лежащих в одной плоскости) пространства.
Декартовой обычно называют прямоугольную систему координат с одинаковыми масштабами по осям.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве.
Длиной или модулем вектора называется длина отрезка, изображающего данный вектор. Длиной нулевого вектора называется число нуль.
Длина вектора на плоскости вычисляется по следующей формуле:

Длина вектора в трехмерном пространстве вычисляется по следующей формуле:

Расстояние между точками A 1 и A 2 можно вычислить по формуле
 |
Едини́чный ве́ктор или орт (единичный вектор нормированного векторного пространства) — вектор, норма (длина) которого равна единице.
 .
. 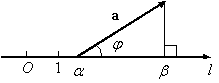
Направление вектора в пространстве определяется углами  , которые вектор образует с осями координат (рис. 12). Косинусы этих углов называются направляющими косинусами вектора:
, которые вектор образует с осями координат (рис. 12). Косинусы этих углов называются направляющими косинусами вектора:  ,
,  ,
,  .
.
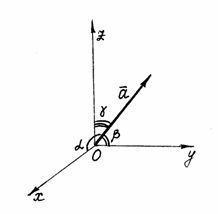
Рис. 12
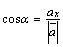 ,
,  ,
,  .
.
 2018-02-13
2018-02-13 1851
1851








