Ответы
1. Понятие поля. Числовые поля Q, R, C. Конечные поля.
-Понятие поля
Полем называют множество элементов, на котором определены две операции. Одна из них называется сложением и обозначается a + b, а другая – умножением и обозначается a · b, даже если эти операции не являются обычными операциями сложения и умножения чисел
-Числовые поля Q, R, C
Для числовых полей очевидно, что сумма нескольких единиц (1 + 1 + … + 1) не может равняться нулю. Следовательно, характеристика этих полей (R, C и Q) равна нулю.
-Конечные поля.
Конечным полем  называется конечное множество элементов, замкнутое по отношению к двум заданным в нем операциям комбинирования элементов. Под замкнутостью понимается тот факт, что результаты операций не выходят за пределы конечного множества введенных элементов. Для конечных полей выполняются следующие аксиомы.
называется конечное множество элементов, замкнутое по отношению к двум заданным в нем операциям комбинирования элементов. Под замкнутостью понимается тот факт, что результаты операций не выходят за пределы конечного множества введенных элементов. Для конечных полей выполняются следующие аксиомы.
2. Поле комплексных чисел. Модуль и аргумент комплексного числа. Формы записи комплексных чисел. Формула Муавра. Нахождение корней n -й степени комплексного числа
-Поле комплексных чисел.
Поле, элементами к-рого являются комплексные (в частности, действительные) числа. Множество комплексных чисел образует Ч. п. тогда и только тогда, когда оно содержит более одного числа и вместе с каждыми числами  и
и  также и
также и  и
и 
-Модуль и аргумент комплексного числа.
Длина вектора, изображающего комплексное число, называется модулем комплексного числа.
Угол φ между осью абсцисс и вектором OM, изображающим комплексное число a + b·i, называется аргументом комплексного числа a + b·i
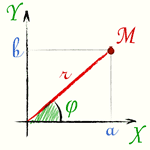
-Формы записи комплексных чисел.
Тригонометрическая и показательная формы
Если вещественную  и мнимую
и мнимую 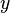 части комплексного числа выразить через модуль
части комплексного числа выразить через модуль  и аргумент
и аргумент  (
( ,
,  ), то всякое комплексное число
), то всякое комплексное число 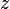 , кроме нуля, можно записать в тригонометрической форме
, кроме нуля, можно записать в тригонометрической форме

Также может быть полезна показательная форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера:
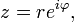
где  — расширение экспоненты для случая комплексного показателя степени.
— расширение экспоненты для случая комплексного показателя степени.
Отсюда вытекают следующие широко используемые равенства:
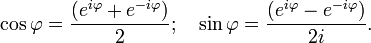
-Формула Муавра.
Эта формула позволяет возводить в целую степень ненулевое комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид:

где  — модуль, а
— модуль, а  — аргумент комплексного числа.
— аргумент комплексного числа.
-Нахождение корней n-й степени комплексного числа.
при вычислении корней  -ой степени из ненулевого комплексного числа:
-ой степени из ненулевого комплексного числа:

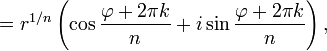

3. Понятие кольца. Кольцо многочленов над полем. Теорема Безу. Основная теорема алгебры. Разложение многочленов на множители в поле R. Нахождение целых корней многочлена.
-Понятие кольца.
Кольцом  называется множество элементов, на котором определены две операции – сложение и умножение, и в
называется множество элементов, на котором определены две операции – сложение и умножение, и в  выполняются следующие аксиомы:
выполняются следующие аксиомы:
1. R.1. Множество  является аддитивной абелевой группой.
является аддитивной абелевой группой.
2. R.2. Для любых двух элементов 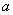 и
и 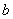 из
из  определено их произведение:
определено их произведение:  (замкнутость операции умножения).
(замкнутость операции умножения).
3. R.3. Для любых трех элементов 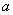 ,
, 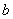 и
и  из
из  выполняется ассоциативный закон, т.е.
выполняется ассоциативный закон, т.е.  и
и  .
.
4. R.4. Для любых трех элементов 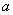 ,
, 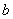 и
и  из
из  выполняется дистрибутивный закон, т.е. справедливы равенства:
выполняется дистрибутивный закон, т.е. справедливы равенства:  и
и  .
.
-Кольцо многочленов над полем.
Поле P называется алгебраически замкнутым, если любой многочлен положительной степени имеет в этом поле корень. Алгебраической замкнутостью обладает поле C, это решается основной теоремой алгебры.
-Теорема Безу.
Если многочлен 

 разделить на двучлен x - a, то в остатке получим число R, равное значению данного многочлена при x = a, т. е. R = Pn(a).
разделить на двучлен x - a, то в остатке получим число R, равное значению данного многочлена при x = a, т. е. R = Pn(a).
Всякий многочлен с любыми комплексными коэффициентами, степень которого не
меньше единицы имеет хотя бы один корень, в общем случае комплексный.
-Разложение многочленов на множители в поле R.
Каждый многочлен, степени большей нуля, разлагается в данном поле в произведение неприводимых множителей единственным образом
-Нахождение целых корней многочлена.
Пусть многочлен записан в каноническом виде  Подставим
Подставим  и освободимся от знаменателей, домножив на наибольшую степень n:
и освободимся от знаменателей, домножив на наибольшую степень n:


Перенесем вправо член 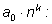

Произведение  делится на целое число m. По условию дробь
делится на целое число m. По условию дробь  несократима, следовательно, числа m и n взаимно просты. Тогда взаимно простыми будут числа m и
несократима, следовательно, числа m и n взаимно просты. Тогда взаимно простыми будут числа m и  Если произведение чисел
Если произведение чисел  делится на m, а множитель
делится на m, а множитель  взаимно прост с m, то второй множитель
взаимно прост с m, то второй множитель  должен делиться на m.
должен делиться на m.
Доказательство делимости старшего коэффициента  на знаменатель n доказывается точно так же, перенося вправо член
на знаменатель n доказывается точно так же, перенося вправо член  и вынося слева множитель n за скобку.
и вынося слева множитель n за скобку.
4. Алгебра матриц
1. Сложение матриц
Определение. Суммой матриц  и
и  одинаковой размерности
одинаковой размерности  называется третья матрица
называется третья матрица  такой же размерности
такой же размерности  , где ее элементы
, где ее элементы  определяются равенством
определяются равенством 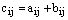 для всех значений индексов.
для всех значений индексов.
2. Умножение матрицы на скаляр
Определение. Произведением скаляра  на матрицу
на матрицу  называется матрица
называется матрица  тех же размеров, что и матрица А, где элементы
тех же размеров, что и матрица А, где элементы  определяются равенством
определяются равенством  , для всех значений индексов.
, для всех значений индексов.
3. Умножение матриц
Определение. Произведением строки длины n на столбец высоты n называется скаляр, вычисляемый по правилу:
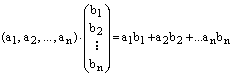
4. Обратная матрица
Определение. Матрица В называется обратной по отношению к матрице А, если

-Кольцо матриц над полем
Пусть 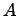 -- произвольное множество, на котором определены две бинарные операции: сложение
-- произвольное множество, на котором определены две бинарные операции: сложение 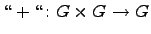 и умножение
и умножение  . Множество
. Множество 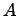 называется кольцом, если
называется кольцом, если
1) относительно сложения 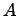 является абелевой группой;
является абелевой группой;
2) операция умножения дистрибутивна, т.е. для любых  справедливы равенства
справедливы равенства  и
и  .
.
Определитель обратимости матрицы
 2018-02-13
2018-02-13 4537
4537







