Связь между матрицами одного и того же линейного оператора в разных базисах

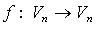Если в базисе линейный оператор имеет матрицу A, в базисе - матрицу B, а S - матрица перехода от первого базиса ко второму, то

Произведение и сумма линейных операторов

Если f и g - линейные операторы пространства с матрицами A и B в базисе , то операторы произведения и суммы 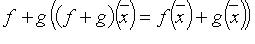- линейные и имеют в том же базисе матрицы BA и A + B соответственно.

Оператор, обратный данному линейному оператору

Линейный оператор называется обратным линейному оператору 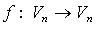, если

Обозначение:

Для существования необходимо и достаточно, чтобы f был невырожденным оператором. Если A - матрица оператора f в некотором базисе, то оператор в том же базисе имеет матрицу .

Характеристический многочлен и его инварианты.

Вопрос

Ненулевой вектор х назовем собственным вектором линейного оператора , если существует такое число l, что выполняется равенство: х = lх.

Число l называется собственным числом или собственным значением оператора .

Т.к. оператор  преобразует пространство само в себя, то матрица этого оператора квадратная. Если базис пространства {e_n}, то

матрица оператора:

Запишем в координатной форме равенство х = lх:

(  - lЕ) х = 0

Эта система линейных однородных уравнений относительно координат искомого вектора х. Т.к. х ¹ 0, то системы должна иметь ненулевое решение. Значит, для этого, должно быть det (A - l E) = 0, или

Уравнение D(l) = 0 называется характеристическим уравнением для линейного оператора , а многочлен

степени n относительно l - характеристическим многочленом.