Теорема об изоморфизме алгебры линейных операторов и алгебры матриц

 

-Теорема об изоморфизме алгебры линейных операторов и алгебры матриц.

Два конечно мерных линейных пространства (над одним и тем же числовым полем) изоморфны тогда и только тогда, когда они имеют одну и ту же размерность.

 

Действительно, если пространства изоморфны , то базису 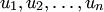пространства соответствует линейно независимая система векторов пространства (см. пункт 3 замечаний 8.6), которую в случае необходимости можно дополнить до базиса пространства (см. теорему 8.2). Следовательно, . Аналогично получаем противоположное неравенство . Таким образом, (необходимость доказана). Достаточность следует из пунктов 4,5 замечаний 8.6. Действительно, пусть пространства и определены над полем и . Тогда, выбрав любые базисы в пространствах и , установим изоморфизмы и , если и — вещественные пространства. Если пространства и определены над полем комплексных чисел, то и . В обоих случаях, согласно пункту 5 замечаний 8.6, пространства и изоморфны. Теорема доказана.

 

 

Связь между матрицами линейного оператора в разных базисах

Определение линейного оператора

 

Преобразование (оператор, отображение) f линейного пространства в себя (запись ) называется линейным, если:

Условия 1 и 2 равносильны соотношению

Матрица линейного оператора

 

Матрица линейного оператора 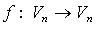в базисе () - матрица

столбцами которой являются столбцы образов базисных векторов оператора f, т. е.

Линейный оператор называется невырожденным, если

Связь между координатами вектора и его образа

 

Если в базисе () имеет координатный столбец - линейный оператор с матрицей A в данном базисе, - координатный столбец вектора , то Y = AX (употребляется также запись ). Более подробно: