Пусть L- это некоторое множество, элементы которого мы удем называть "векторами", P- некоторое(числовое поле). Пусть так же выполняются следующие условия.
1. В L определена операция сложения элементов.
2. В Lопределена операция умножения элемента на число из P.
3. Эти операции удовлетворяют законам дистрибутивности.
Тогда говорим, что L образует линейное пространство над полем P относительно операций сложений и умножней.
Произведение линейных операторов: определение и свойства.



Критерии невырожденности линейного оператора.

Ядро, образ, ранг и дефект линейного оператора. Связь ранга и дефекта
ВНИМАНИЕ, ДЛЯ ПОЛНОГО ОЗНАКОМЛЕНИЕ ПРОСМОТРИТЕ ВОПРОС 33!
Ядро и область значений линейного оператора
Ядро оператора: 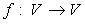 - множество, обозначаемое Ker f:
- множество, обозначаемое Ker f:
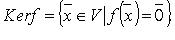
Область значений (образ) оператора 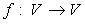 - множество, обозначаемое Im f:
- множество, обозначаемое Im f:
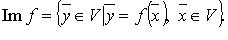
Множества Ker f и Im f являются подпространствами пространства V.
Ранг оператора 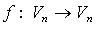 (обозначение: dim Im f) - ранг матрицы A линейного оператора f,
(обозначение: dim Im f) - ранг матрицы A линейного оператора f,
dim Im f = rank A.
Дефектом оператора 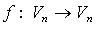 называют dim Ker f,
называют dim Ker f,
dim Im f + dim Ker f = n.
Матрица линейного оператора. Теорема о координатах образа вектора при линейном преобразовании
Линейный оператор A действует из n -мерного линейного пространства X в m -мерное линейное пространство Y.
В этих пространствах определены базисы e = {e 1,..., e n } и f = {f 1,..., f m }.
Пусть A (e i) = a 1 i ·f 1 + a 2 i ·f 2 +...+ a m i ·f m — разложение образа i -го базисного вектора базиса e пространства X по базису f пространства Y, i = 1, 2,..., n.
Матрицей линейного оператора в базисах e, f называется матрица A, столбцами которой являются координаты образов базисных векторов базиса e в базисе f, A = { a i j } = { A (e j) i }:

Координаты образа y = A (x) и прообраза x связаны соотношеннием:
y = A · x,
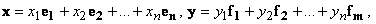

-Теорема о координатах образа вектора при линейном преобразовании.
Образ вектора х равен произведению матрицы линейного оператора на столбец его координат: если у = А (х), то 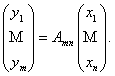
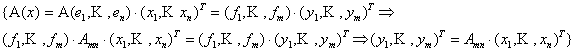
 2018-02-13
2018-02-13 2750
2750
