Метод хорд і метод дотичних

Метод хорд і метод дотичних є різновидами методу ітерації при спеціальному виборі функції . В методі хорд 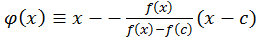, де  – так звана нерухома точка, в якості береться той з кінців відрізку , де , інший кінець цього відрізку береться за початкове наближення , ітерації будуються по формулі

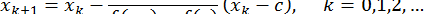
(до спільного знаменника не зводити! Чому?).

     У методі дотичних , за початкове наближення вибирається один з кінців відрізку , саме той, де . Робоча формула методу має вигляд

Для закінчення процесу ітерацій в методі дотичних можна використати наступну оцінку точності

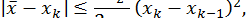
де

   а

Крім того, оцінювати похибку наближень в усіх методах можна за загальною оцінкою (8).

В методах хорд і дотичних корінь бажано відокремити так, щоб 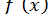та  зберігали знак на [a, b] (інакше метод може виявитися непридатним).

З оцінок точності методів видно, що метод дотичних (Ньютона) збігається швидше за інші. Це - метод другого порядку точності.

ПРИКЛАД 19. Методом хорд і методом дотичних знайти з точністю до позитивний корінь рівняння

В методі хорд

.

Отже, .

В методі дотичних ; ; .

Помітимо, що в методі дотичних початкове наближення  виявилося найгрубішим, цим пояснюється велика кількість (порівняно з іншими методами) ітерацій.

Комбінований метод

    Оскільки наближення до кореня, що отримуються методом хорд та дотичних, лежать по різні сторони від кореня , то дуже вигідно поєднувати ці методи. Отримуємо так званий комбінований метод, він застосовується на кожному кроці до нового відрізку, або до , якщо правий кінець нерухомий, або до , якщо залишається нерухомим лівий кінець. Очевидно, що середина відрізку є наближенням до кореня з точністю

Так, в даному прикладі після першого кроку отримуємо

;   далі,

;   далі,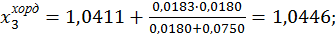

.

Довжина останнього відрізку дорівнює , отже, значення  є наближенням до кореня з точністю .