Метод простої ітерації для уточнення коренів рівняння (6) полягає в наступному. Рівняння (6) зводиться до вигляду

причому має бути виконана умова збіжності
 для
для  .
.
На відрізку  вибираємо початкове наближення
вибираємо початкове наближення  (
( краще брати з середньої третини відрізку
краще брати з середньої третини відрізку  , інакше похибка округлення може вивести нас за межі того відрізку, де виконується умова збіжності) і знаходимо подальші наближення до кореня за формулою
, інакше похибка округлення може вивести нас за межі того відрізку, де виконується умова збіжності) і знаходимо подальші наближення до кореня за формулою

Ітерації  обчислюємо до виконання умови
обчислюємо до виконання умови
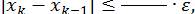
тоді з оцінки точності цього методу

випливає, що  .
.
Помітимо, що у випадку, коли  і
і  , послідовні наближення збігаються до кореня, коливаючись відносно кореня (
, послідовні наближення збігаються до кореня, коливаючись відносно кореня ( праворуч,
праворуч,  ліворуч,
ліворуч,  праворуч і так далі). В цьому випадку
праворуч і так далі). В цьому випадку

і, отже, знаки наближення  , що встановилися, обов’язково належать до точного значення кореня
, що встановилися, обов’язково належать до точного значення кореня  .
.
ПРИКЛАД 17. Методом простої ітерації знайти з точністю  позитивний корінь рівняння
позитивний корінь рівняння

Зведемо це рівняння до вигляду 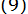 :
:
 та
та
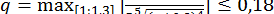 .
.
Візьмем  , тоді
, тоді
 ;
; 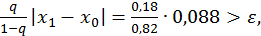
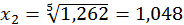 ;
;  .
.
Значить,  з точністю
з точністю 
ПРИКЛАД 18. Методом простої ітерації знайти з точністю до  позитивний корінь рівняння
позитивний корінь рівняння

Раніше було знайдено, що 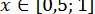 . Далі,
. Далі,  , тобто
, тобто
 ;
;  .
.
Для всіх 
 . Значить, наближення
. Значить, наближення  збігаються до кореня коливаючись
збігаються до кореня коливаючись

 ;
;  ;
;
 ;
; 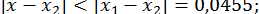
 ;
; 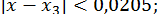
 ;
; 
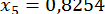 ;
; 

На швидкість збіжності методу ітерацій впливає вибір початкового приближения  а також величина
а також величина  .
.
Зведення рівняння (6) до вигляду (9) можна здійснити різними способами. Так, в прикладі 17, безпосередньо виражаючи  з рівняння, отримуємо
з рівняння, отримуємо  ;
;
або  ;
;
або  та ін.
та ін.
Очевидно, при відшукуванні кореня, що належить відрізку  , можна ітерувати перше з цих рівнянь, але воно не придатне для кореня з відрізку
, можна ітерувати перше з цих рівнянь, але воно не придатне для кореня з відрізку  .
.
У разі, якщо це рівняння має вигляд  , але в околі шуканого кореня
, але в околі шуканого кореня  має місце нерівність
має місце нерівність

то замінюємо це рівняння еквівалентним
 ,
,
де  , для цього рівняння процес ітерації збігатиметься, оскільки
, для цього рівняння процес ітерації збігатиметься, оскільки

Так, при знаходженні коренів рівняння  слід ітерувати рівняння
слід ітерувати рівняння

Вельми корисним на практиці виявляється наступний спосіб зведення рівняння (6) до вигляду (9). Нехай корінь  рівняння (6) належить відрізку
рівняння (6) належить відрізку  і для
і для  виконується нерівність
виконується нерівність
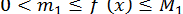
(важливо, що похідна зберігає знак на  ).
).
Покладемо тоді

умова збіжності виконується, оскільки

Наприклад, для рівняння  маємо
маємо  для будь-якого
для будь-якого  , і отже, для відшукування кореня з цього відрізку можна ітерувати рівняння
, і отже, для відшукування кореня з цього відрізку можна ітерувати рівняння

при цьому  . Виходячи з
. Виходячи з  (приклад 17) для досягнення точності
(приклад 17) для досягнення точності  потрібно виконати 7 ітерацій (у прикладі 17 всього дві ітерації).
потрібно виконати 7 ітерацій (у прикладі 17 всього дві ітерації).
Це показує, як важливо при зведенні рівняння (6) до вигляду (9) добитися, щоб  було якнайменшим.
було якнайменшим.
 2018-02-13
2018-02-13 601
601








