Метод виключення Гаусса. Модифікації, або схеми обчислень

Один з найбільш поширених точних методів являється метод виключення Гаусса. Існує декілька модифікацій цього методу: схема єдиного ділення, схема повного виключення, схема з вибором головного елементу по всій матриці, по рядку, по стовпцю, компактна схема та інші. Суть цих модифікацій з’ясуємо на прикладах.

ПРИКЛАД 24. Розв’язати систему

Спочатку розв’яжемо систему за схемою єдиного ділення. Поділимо перше рівняння на ( – провідний елемент), отримаємо провідне рівняння першого кроку

(обчислення проводимо з трьома десятковими знаками).

За допомогою провідного рівняння виключаємо з другого та третього рівнянь, для цього помножимо провідне рівняння спочатку на та віднімемо з другого, потім - на 0,30 та віднімемо з трєтього, отримаємо

Друге рівняння цієї системи поділимо на коефіціент при 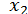(він відрізняється від нуля), отримаємо провідне рівняння другого кроку

за допомогою нього виключаємо з останнього рівняння

Звідси

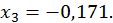
Об’єднуємо всі провідні рівняння; отримаємо трикутну систему

Побудова трикутної системи називається прямим ходом схеми. Зворотний хід - розв’язання отриманої трикутної системи (знизу вгору)

; ; .

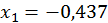Звернемо увагу, що якщо провідний елемент опиниться рівним нулю, варто переставити рядки так, щоб елемент в лівому верхньому куті відрізнявся від нуля (зайвих перестановок не робити!).

Схема повного виключення характеризується тим, що на -му кроці невідоме виключається з усіх попередніх і наступних рівнянь.

Для розглянутої системи таблиці коефіцієнтів будуть такими:

після першого кроку:

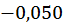
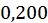
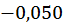
після другого кроку:

після третього кроку:

Очевидно, в схемі повного виключення зворотнього ходу не треба, оскільки ми приходимо до системи з діагональною (одиничною) матрицею.

А тепер розглянемо схему з вибором головного елементу. Спочатку знаходимо найбільший по модулю елемент матриці системи, для нашої системи це . Переставляємо рядки і стовпці рівнянь так, щоб найбільший по модулю коеффіцієнт стояв у верхньому лівому куті, тобто

і проводимо, як і раніше, перший крок виключення, тоді

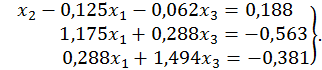
Далі, вибираємо максимальний за модулем елемент у системі без першого рівняння і ставимо його в лівому верхньому куті

Другий крок виключення дає

За допомогою зворотнього ходу з провідних рівнянь ми отримаємо значення невідомих:

; ;

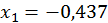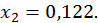
В схемах з вибором головного елементу по рядку або стовпцю максимальний за модулем елемент вибирається відповідно в рядку або стовпці.

Відмітимо, що при програмуванні вищевказаних методів варто брати до уваги, що операція ділення на ЕОМ більш трудомістка, і тому при побудові провідного рівняння треба не ділити на провідний елемент, а помножити на елемент, зворотний провідному.

Схема з вибором головного елементу по всій матриці менш чутливі до помилок округлення, ніж інші, але вибір головного елемента в матриці (двовимірному масиві) на ЕОМ достатньо трудомісткий, тому часто використовуються на ЕОМ схеми з вибором головного елемента в рядку або стовпці (одновимірному масиві).

Зауважимо також, що в системах з діагональним переважанням, тобто системах, для яких

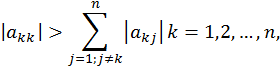
помилки округлення не накопичуються.

В системі (17) маємо діагональне переважання:

; ; ,

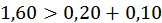тому значення невідомих, знайдених за допомогою різних модифікацій метода Гаусса, співпадали з точністю до трьох десяткових знаків. Однак в загальному випадку при розв’язанні системи за допомогою схеми з вибором головного елементу помилка округлення менше. Проілюструємо це на прикладі; будемо виконувати обчислення з трьома значущими цифрами.

Схема єдиного ділення для системи

дає наступні значення для невідомих: ;

За допомогою схеми з вибором головного елементу отримаємо

та ; .

Як правило, чутливими до помилок округлення є системи з великим розкидом за абсолютною величиною коефіцієнтів. Корисним може бути вирівнювання коефіцієнтів. Покажемо ефект вирівнювання на прикладі. Нехай дана система

;

її розв’язок ; . Проводимо обчислення з чотирма значущими цифрами за допомогою схеми єдиного ділення; отримаємо

Проведемо попередньо вирівнювання коефіцієнтів

або

за допомогою схеми єдиного ділення для системи

знайдемо ; та ; .

Метод Холецького. Якщо в матриці всі головні мінори не дорівнюють нулю, існує та є єдиним розкладення де

Системи з такою матрицею можна розв’язати методом Холецького. Елементи матриць та знаходять з рівності елементів матриць та які стоять на однакових місцях. Далі розв’язують дві трикутні системи

ПРИКЛАД 25. Розв’язати систему (17) методом Холецького.

Маємо

З рівності перших стовпців знаходимо

З рівності других стовпців:

З рівності третіх стовпців:

Розв’язання системи дає:

Компактна схема методу Гаусса базується на схемі єдиного ділення. Аналізуючи процес обчислення по схемі єдиного ділення, бачимо, що

де – елемент початкової матриці, – елемент допоміжної матриці після -го кроку, – елементи провідного рівняння -го кроку.

Позначимо через елементи першого стовпця кожної допоміжної матриці, тобто . Тоді можемо записати

Зокрема,

За формулами (18') визначаються, очевидно, і вільні члени перетворюваних рівнянь. Схема проведення прямого ходу за формулами , називається компактною. На більшості сучасних ЕОМ суми типу скалярних добутків, які входять в и , можна розрахувати з подвійною точністю, що забезпечує високу точність методу.

Розв’яжемо за допомогою компактної схеми Гаусса систему (17).

; ; ;

; ; ; ;

;

; ; ;

;

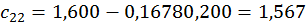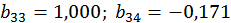тобто отримуємо дві матриці:

причому (перші три стовпця утворюють матрицю ).

Залишається виконати зворотний хід для системи, коефіцієнти якої – елементи матриці .

Надзвичайно ефективним є метод виключення Гаусса для розв’язання тридіагональних систем (особливо з діагональним переважанням), які часто виникають при розв’язанні диференціальних рівнянь різницевими методами. Метод виключення для тридіагональних систем називають методом “прогонки”. Розглянемо його. Нехай дана тридіагональна система

Перше рівняння можна записати у вигляді

де , . По індукції можна показати, що формула має місце при будь-якому , причому:

Пряма прогонка (прямий хід) при розв’язанні системи – це обчислення коефіцієнтів , , , за рекурентними формулами . Зворотня прогонка – знаходження невідомих , починаємо з .