Розглянемо тепер наближені методи розв’язання лінійних систем - метод простої ітерації, метод Зейделя, метод верхньої релаксації. Суть цих методів полягає в наступному. Спочатку система (16) яким-небудь чином приводиться до вигляду

де  – матриця,
– матриця,  – вектор. Потім, виходячи з довільного (!) вектора
– вектор. Потім, виходячи з довільного (!) вектора  , будується ітераційний процес. У методі простої ітерації наближення знаходяться за формулами:
, будується ітераційний процес. У методі простої ітерації наближення знаходяться за формулами:




У методі Зейделя при знаходженні координати  -го наближення використовуються вже знайдені координати
-го наближення використовуються вже знайдені координати  цього наближення, тобто:
цього наближення, тобто:




Методи простої ітерації і Зейделя збігаються, якщо матриця  така, що
така, що
або 
або 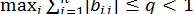 .
.
Для методу ітерації має місце оцінка

тому для досягнення точності  треба добитися виконання нерівності
треба добитися виконання нерівності

Для методу Зейделя гарних оцінок точності немає, тому наближення будують до тих пір, поки дві сусідні ітераціі  і
і  не співпадуть із заданою точністю.
не співпадуть із заданою точністю.
Очевидно, якщо матриця 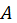 з діагональним переважанням, розділимо перше рівняння на
з діагональним переважанням, розділимо перше рівняння на  і залишимо ліворуч тільки
і залишимо ліворуч тільки  , виразимо з першого рівняння
, виразимо з першого рівняння  через
через  ,
,  ,
,  ,
,  ; аналогічно виразимо
; аналогічно виразимо  з другого рівняння і так далі. Тим самим ми зведемо систему до вигляду (21), причому умова збіжності буде виконана. Діагонального переважання в матриці A можна добитися, помноживши систему (16) на матрицю
з другого рівняння і так далі. Тим самим ми зведемо систему до вигляду (21), причому умова збіжності буде виконана. Діагонального переважання в матриці A можна добитися, помноживши систему (16) на матрицю  , яка є грубим наближенням
, яка є грубим наближенням
до оберненої матриці  При невеликих
При невеликих  можна не знаходити
можна не знаходити  , а будувати систему, рівносильну даній системі, з діагональним переважанням, рівняння якої є лінійними комбінаціями рівнянь даної системи.
, а будувати систему, рівносильну даній системі, з діагональним переважанням, рівняння якої є лінійними комбінаціями рівнянь даної системи.
ПРИКЛАД 27. Розв’язати методом простої ітерації і методом Зейделя з точністю до  систему
систему

Зводимо систему до вигляду, придатного для застосування методу ітерацій, причому бажано, щоб 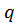 було якомога ближче до нуля, а не тільки просто менше 1. Будуємо спочатку систему, рівносильну даній системі, з діагональним переважанням:
було якомога ближче до нуля, а не тільки просто менше 1. Будуємо спочатку систему, рівносильну даній системі, з діагональним переважанням:

Звідси

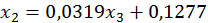


Вибираємо початкове наближення (можна узяти вільні члени):
 ;
;  ;
;  .
.
Тоді
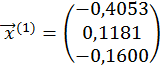 ;
;
 ;
;
 ,
, 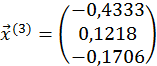 ,
,  .
.

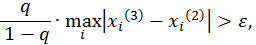

Точність досягнута, 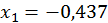 ;
;  ;
;  .
.
Ітерації за методом Зейделя будуть наступними:
 ;
;  ;
;  ;
;
 ;
; 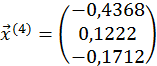 .
.
Відмітимо, що метод Зейделя, як правило, збігається швидше, ніж метод ітерації, хоча може бути і навпаки.
Як вже відзначалося, діагональне переважання в системі (16) є достатньою умовою збіжності методів Зейделя і методу простої ітерації. Проте цю умову можна значно послабити, а саме, повинна виконуватися умова

причому принаймні для одного  (в одному рівнянні) має бути строга нерівність.
(в одному рівнянні) має бути строга нерівність.
Так, методи простої ітерації і Зейделя для системи

яка є рівносильною системі (21), збігаються, але збіжність дуже повільна (для досягнення точності  , виходячи з
, виходячи з  ;
;  ;
;  , вимагається виконати більше 500 ітерацій).
, вимагається виконати більше 500 ітерацій).
Розглянемо ще один наближений метод розв’язання лінійних систем - метод верхньої релаксації. Суть цього методу полягає в наступному. Матриця  подається у вигляді суми
подається у вигляді суми

де 

Обидві частини наведеної таким чином системи

помножимо на число  що називається релаксаційним параметром, а потім додамо до них
що називається релаксаційним параметром, а потім додамо до них 

aбо

Покладемо у формулі (22)  Маємо
Маємо

або

Отримали метод Зейделя.
У разі довільного 

Далі, помножимо (22) на 



де

Встановлено, що для збіжності ітераційного процесу

необхідно, щоб  Для деяких класів систем лінійних алгебраїчних рівнянь ця вимога до параметра релаксації є і достатньою (наприклад, для систем, в яких
Для деяких класів систем лінійних алгебраїчних рівнянь ця вимога до параметра релаксації є і достатньою (наприклад, для систем, в яких  симетрична позитивно визначена матриця).
симетрична позитивно визначена матриця).
Проте природно розпорядитися параметром  так, щоб спектральний радіус матриці
так, щоб спектральний радіус матриці  був найменшим. Усі елементи матриці
був найменшим. Усі елементи матриці  залежать від
залежать від  , значить, власні числа
, значить, власні числа  залежать від
залежать від  треба підібрати таке
треба підібрати таке  щоб найбільше за модулем власне число при цьому
щоб найбільше за модулем власне число при цьому  набувало мінімального значення, меншого за одиницю:
набувало мінімального значення, меншого за одиницю:

У загальному випадку задача знаходження оптимального  не розв’язана, і в практичних розрахунках застосовують метод проб і помилок. Проте для деяких важливих класів задач значення
не розв’язана, і в практичних розрахунках застосовують метод проб і помилок. Проте для деяких важливих класів задач значення  знайдене. Суттєво відмітити, що
знайдене. Суттєво відмітити, що 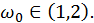
При  розглянутий метод називається методом верхньої релаксації.
розглянутий метод називається методом верхньої релаксації.
При  розглянутий метод називається методом нижньої релаксації. Він взагалі кажучи не ефективний.
розглянутий метод називається методом нижньої релаксації. Він взагалі кажучи не ефективний.
ПРИКЛАД 28. Розв’язати систему (17) методом верхньої релаксації.
Маємо


Далі,


 ,
,
де
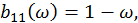








Нехай  найбільше власне число матриці
найбільше власне число матриці  дорівнює 0,17.
дорівнює 0,17.
Метод верхньої релаксації при 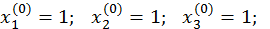 дає наступні результати:
дає наступні результати:





Нехай  найбільше власне число матриці
найбільше власне число матриці  дорівнює 0.657.
дорівнює 0.657.
Метод верхньої релаксації при 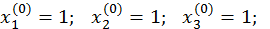 дає наступні результати:
дає наступні результати:

. . . . . . . . . . 




Задачі
Розв’язати розглянутими методами з точністю до  наступні лінійні системи.
наступні лінійні системи.
71. 
72. 
73. 
74. 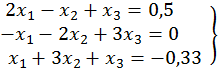
75. 
76. 
77. 
78. 
79. 
80. 
81. 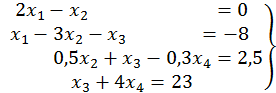
Знайти з точністю до  визначник і обернену матрицю для наступних матриць.
визначник і обернену матрицю для наступних матриць.
82. 
83. 
84. 
 2018-02-13
2018-02-13 1007
1007
