Розв’язання нелінійних систем

 Для розв’язання нелінійних систем можна використати також метод ітерацій. Після того, як буде знайдено початкове наближення 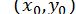  до розв’язку 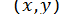, система зводиться до вигляду

                                  (23)

при цьому функції 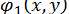и 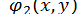 повинні задовольняти умові збіжності

 

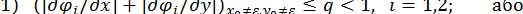
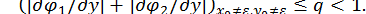
 (в умовах збіжності суми абсолютних величин похідних не повинні перевищувати 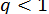в деякому околі розв’язку 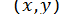, але оскільки початкове наближення  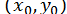- з околу розв’язку , то в умовах збіжності можна узяти окіл початкової точки). Послідовні наближення до розв’язку визначаються за формулами:

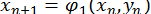
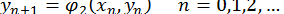
Має місце наступна оцінка точності методу

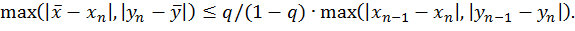
ПРИКЛАД 29. Знайти з точністю до 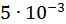 методом ітерацій розв’язок системи 

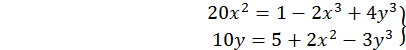
Початкове наближення було знайдене раніше:

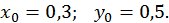
Для застосування методу ітерації зводимо систему до вигляду :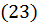

 

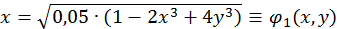
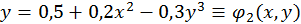
Умова збіжності методу ітерацій виконується. Дійсно,

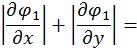
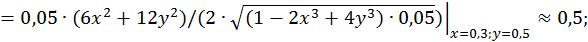
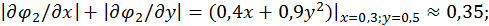
і можна узяти .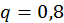

Знаходимо перше наближення і оцінюємо його точність: 

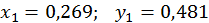
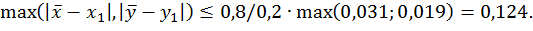
Аналогічно отримуємо

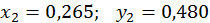
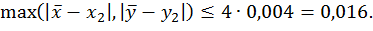
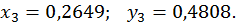
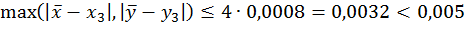
Значить, .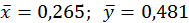

Побудова ітеруючих функці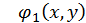й  и 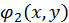 вимагає деякого досвіду і винахідливості, можна рекомендувати наступний прийом. Візьмемо  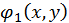та 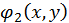у вигляді

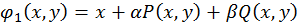
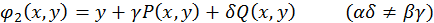
і визначимо коефіцієнти 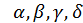  з умов

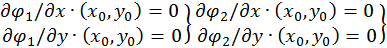
(умова збіжності виконується).

Для даного прикладу цей спосіб дає:

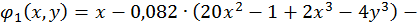
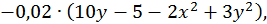
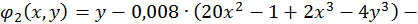
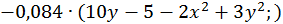
Задачі

Знайти методом ітерацій з точністю до  один розв’язок нелінійних систем в задачах 46 - 57.

СИНГУЛЯРНЕ  РОЗКЛАДЕННЯ  МАТРИЦІ

Сингулярне розкладення матриці (SingularValueDecomposition, SVD) є зручним методом при роботі з матрицями. Сингулярне розкладення показує геометричну структуру матриці і дозволяє наочно представити наявні дані. Сингулярне розкладення матриці дуже корисне при розв’язанні різних завдань, наприклад:

- стискування і розпізнавання зображень;

- розв’язок лінійних систем рівнянь алгебри;

- обчислення визначників;

- обчислення рангу матриці;

- дослідження обумовленості матриці;

- наближення методом найменших квадратів.