Необходимо перейти от системы неравенств к системе уравнений.
Для этого необходимо ввести новые переменные.
Система (5) преобразуется:
 |
x1*0,8+ x2*0,8+x3=100
x1*0,2+ x2*0,1+x4=26 (8)
x1*0,15+ x2*0,05+x5=15
x2*0,1+x6=10
xi≥0 i=1..6
Симплекс метод
Симплекс метод решения задач линейного программирования основан на переходе от одного опорного плана к другому, при котором значение целевой функции возрастает (для max) или убывает (для min) (при условии, что данная задача имеет оптимальный план, и каждый ее опорный план является невырожденным). Указанный переход возможен, если известен какой-нибудь исходный опорный план.
Для применения симплекс метода необходимо, чтобы знаки в ограничениях были вида ≤, а компоненты вектора b - положительны.
Необходимо выполнить следующие шаги:
На примере нахождения максимального критерия
1. Найти опорный план.
2. Составляют симплекс-таблицу. В общем виде:
| -Cb | БП | x1 | x2 | ... | xr | xr+1 | xj | xn | b |
| -C1 -C2 ... -Ci ... -Cr | x1 x2 ... xi ... xr | 1 0 ... 0 ... 0 | 0 1 0 0 | 0 0 ... 0 ... 1 | a1,r+1 a2,r+1 ... ai,r+1 ... ar,r+1 | a1j a2j ... aij ... arj | a1n a2n ... ain ... arn | b1 b2 ... bi ... br | |
| ƒ | 0 | 0 | ... | 0 | Cr+2 | Cj | Cn | C0 |
3. В нижней строчке симплекс-таблицы необходимо отыскать отрицательные числа (не считая коэффициент Со). Если таких чисел нет, то данное базисное решение является оптимальным.
4. Пусть элемент Сj<0,тогда в j-ом столбце необходимо найти положительный элемент. Если все коэффициенты этого столбца отрицательные, то решения не существует.
5. Если положительный коэффициент в j-ом столбце один, то выбранную строку с номером i надо поделить все коэффициенты на числоaij.Результат деления записываем в новую симплекс-таблицу. Если же положительных коэффициентов несколько, необходимо составить отношение bi/aij и из полученных значений выбрать наименьшее, соответствующее i -ой строке.
6. В новой симплекс-таблице в столбце базисных неизвестных вместо xi пишется xj. Продолжается заполняться таблица. В столбце с номером j необходимо получить нули (включая строку с целевой функцией). Для этого надо умножить i -ую записанную строку (разрешающую) на нужное число и сложить с остальными строками - воспользоваться методом Гаусса или правилом четырехугольника. В результате осуществится переход к новому базису, при этом значение целевой функции увеличится.
7. Повторять пункты 3-6 до тех пор, пока не найдем оптимальное решение.
Правило четырехугольника:
Необходимо построить четырехугольник на диагонали, соединяющей исходный элемент с разрешающим. Тогда новое значение элемента будет равно
((прежнее значение * разрешающий элемент) -(произведение элементов на противоположной диагонали))/(разрешающий элемент).
Для нашей задачи:
Опорный план является оптимальным, если для задачи максимизации все его оценки неотрицательны (для max).
1. Первый опорный план x(1)=(0,0,100,26,15,10)
Видно, что не все оценки положительны, значит, опорный план не является оптимальным.
Будем увеличивать х1 т.к. ее увеличение вызовет наибольшее увеличение критерия. Предположим, что 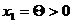 , тогда:
, тогда:
Θ*0,8+ x2*0,8+x3=100
Θ *0,2+ x2*0,1+x4=26
Θ *0,15+ x2*0,05+x5=15
x2*0,1+x6=10
Запишем новый опорный план: 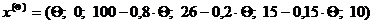 . Все оценки опорного плана должны быть ≥0
. Все оценки опорного плана должны быть ≥0
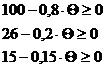 =>
=> 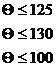
При увеличении 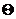 , первой перестает выполнять условие неотрицательности переменная
, первой перестает выполнять условие неотрицательности переменная 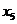 , т.к. она первая обращается в ноль. Значит выведем из базиса
, т.к. она первая обращается в ноль. Значит выведем из базиса 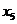 . Теперь базисными переменными являются
. Теперь базисными переменными являются 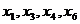 , а свободными
, а свободными 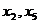 . Для анализа этого плана выразим функцию цели через новые переменные.
. Для анализа этого плана выразим функцию цели через новые переменные.
В симплекс-таблице:
Наименьшее значение коэффициента Ci = -100, значит, выбираем столбец x1. Из отношений bi/ai1 видно, что наименьшее из них для i=5 (третьей строки), следовательно, заменяем переменную x5 .
| Cb | БП | x1 | x2 | x3 | x4 | x5 | x6 | b |
| 0 0 0 0 | x3 x4 x5 x6 | 0.8 0.2 0.15 0 | 0.8 0.1 0.05 0.1 | 1 0 0 0 | 0 1 0 0 | 0 0 1 0 | 0 0 0 1 | 100 26 15 10 |
| ƒ | -100 | -80 | 0 | 0 | 0 | 0 | 0 |
Разрешающий элемент в нашем случае будет на пересечении столбца x1 и строки x5
После преобразований методом Гаусса или правилом четырехугольника получаем вторую симплекс таблицу:
2. Второй опорный план x(2)=(100,0,20,6,0,10)
| Cb | БП | x1 | x2 | x3 | x4 | x5 | x6 | b |
| 0 0 100 0 | x3 x4 x1 x6 | 0 0 1 0 | 0.5(3) 0.0(3) 0.(3) 0.1 | 1 0 0 0 | 0 1 0 0 | -5.(3) -1.(3) 6.(6) 0 | 0 0 0 1 | 20 6 100 10 |
| ƒ | 0 | -46.(6) | 0 | 0 | 666.(6) | 0 | 10000 |
Аналогично определяем следующую замену: x3 на x2
3. Третий опорный план x(3)=(87.5,37.5,0,0,0,0)
| Cb | БП | x1 | x2 | x3 | x4 | x5 | x6 | b |
| 80 0 100 0 | x2 x4 x1 x6 | 0 0 1 0 | 1 0 0 0 | 1.875 -0.062 -0.625 -0.188 | 0 1 0 0 | -10 -1 10 1 | 0 0 0 1 | 37.5 4.75 87.5 6.25 |
| ƒ | 0 | 0 | 87.5 | 0 | 200 | 0 | 11750 |
Так как все Ci≥0, то данный опорный план оптимальный
Получили тот же ответ: x1=87.5; x2=37.5 Прибыль = 11750 руб
Графически мы прошли по точкам многоугольника области возможных значений в направлении от начальной точки (первого опорного плана (1)) в сторону увеличения критерия (по градиенту) по точкам (1)→(2)→(3) см. рис. 2
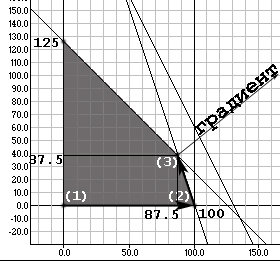
|
 2018-02-13
2018-02-13 232
232








