2018-02-13
397
Зададим на отрезке 
(а и b – конечные числа) неотрицательную непрерывную функцию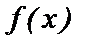 
. Изобразим ее график и определим понятие площади фигуры, ограниченной кривой 
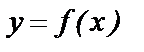, осью 
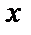, прямым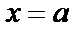и 
и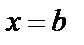 
и вычислим эту площадь. Проведем разбиение отрезка 
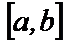на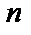 
частей точками 
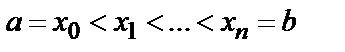, выберем на каждом из полученных отрезков 
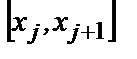(j = 0, 1, …, n –1) по произвольной точке 
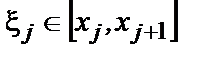определим значения 
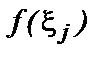функции в этих точках и составим сумму: 
которую называют интегральной суммой и которая равна сумме площадей прямоугольников. Будем теперь стремить все 
к нулю, причем так, чтобы максимальный (самый большой) частичный отрезок разбиения стремиться к нулю. Если при этом величина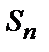 
стремиться к определенному пределу 
, не зависящему от способов разбиения и выбора точек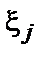 
. Тогда величину 
назовем площадью нашей криволинейной фигуры. Т. о.:
.
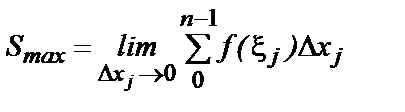Отвлекаясь от операции нахождения площади, будем рассматривать эту операцию как нахождение некоторого числа 
по данной функции 
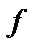, заданной на отрезке 
: 
.
Определенным интегралом от функции на отрезке 
называется предел интегральной суммы, когда максимальный частичный отрезок разбиения стремиться к нулю.
Пусть задана непрерывная на 
функция 
и пусть 
есть ее первообразная. Теорема Ньютона-Лейбница утверждает справедливость следующего равенства: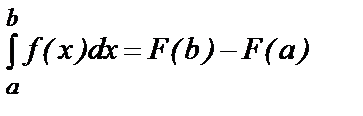 
.
Основные методы интегрирования
Интегрирование заменой переменной (подстановкой)
Пусть функция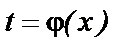 
определена и дифференцируема на некотором множестве 
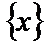, и пусть 
множество всех значений этой функции. Пусть далее для функции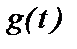 
существует на множестве 
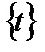первообразная функция 
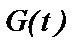, т. е. 
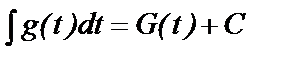. Тогда всюду на множестве 
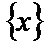для функции 
существует первообразная функция, равная 
, т. е.
.
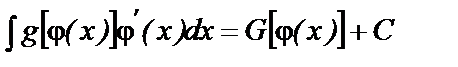Пусть нам требуется вычислить интеграл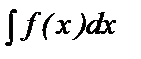 
и можно выбрать в качестве новой переменной функцию 
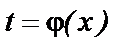так, что 
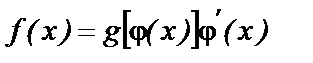, причем 
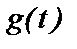легко интегрируется т.е.:
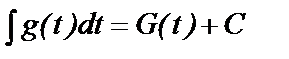и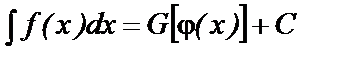 
– этот прием вычисления называется интегрированием путем замены переменной.
