Интегрирование по частям

Пусть каждая из функций  и  дифференцируема на множестве  и, кроме того, на этом множестве существует первообразная для функции . Тогда на множестве  существует первообразная и для функции , причем справедлива формула

.

КИНЕМАТИКА ПАСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬГО ДВИЖЕНИЯ. КОНФИНДЕКСАЛЬНОЕ И НОРМАЛЬНОЕ УСКОРЕНИЕ

Общая прямая задача кинематики:

По известной зависимости радиуса-вектора от времени необходимо определить, векторы скорости и ускорения 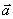и их модули v и а, нормальную и тангенциальную 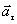составляющую ускорения, радиус кривизны траектории R.

Общая обратная задача кинематики:

По известным векторам скорости или ускорения 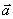необходимо восстановить вид траектории, т.е. найти радиус-вектор , а затем все остальные параметры траектории, указанные в пункте 1.

Частная прямая задача кинематики:

По известной зависимости пути от времени необходимо найти скорость и ускорение тела. В этом случае можно определить лишь модуль скорости и ускорения:

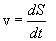и .

Векторы , , , 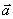а также и 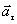в этих задачах не могут быть определены.

Частная обратная задача кинематики:

По известным зависимостям скорости или ускорения необходимо восстановить зависимость пути от времени :

.