2018-02-13
280
Рассмотрим распространение плоской волны через границу двух сред. Опыт показывает, что существует отраженная волна и преломленная. На границе двух диэлектриков должно выполняться условие:
|
|
Это условие следует из теоремы о циркуляции:
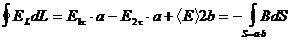
Поскольку это равенство должно выполняться в любой момент времени t и в любой точке x:
Вывод:
Частота света при переходе из одной среды в другую не изменяется.
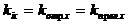
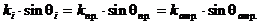
Напомним, что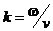 
- волновой вектор.
; 
¾ закон отражения.
Закон преломления
Вспомним, что 
где 
¾ абсолютный показатель преломления
- относительный показатель преломления второй среды относительно первой. Падающий луч, преломленный и перпендикуляр, восстановленный в точке падения, лежат в одной плоскости.
Этот закон выполняется для любой поляризации. Характеризует направление распространения, но ничего не говорит об интенсивности. Вернемся к законам преломления и отражения.
|
|
Если 
> 
то sin i > sin r и i > r. Пустим луч вдоль поверхности т.е. 
. Тогда 
- предельный угол преломления.
Лучи под углом большим в среду 2 проникать не будут.
Полное внутреннее отражение. Рассмотрим обратную ситуацию. При углах падения больших rпред луч будет возвращаться в среду 2. При углах падения света из более плотной среды в менее плотную, заключенных в пределах от rпред до p ¤2 световая волна полностью возвращается в более плотную среду. Это явление называется полным внутренним отражением. Применение: в волоконных линиях связи, интегральных оптических схемах, в оптических призмах ПВО и т.п.
Нарушение полного внутреннего отражения. Оказывается, что свет все-таки проникает в среду 1, но быстро затухает, Если на расстоянии меньше l поместить еще одну среду, то свет будет переходить в нее. Это явление называется нарушением полного внутреннего отражения. Оно называется оптическая связь.
Ðàçäåë 2. Интерференция света.
Сложение волн.
|
Рис.3.1. Две волны |
|
Рис.3.2. Колебания в точке P происходят в одном направлении. |
Пусть в некоторой точке P встречаются две одинаковые монохроматические волны. Одна, например, приходит из точки O1, а вторая из точки O2. Направление колебаний вектора Е у них совпадает:
E1=E01ei(wt+j1) (3.1)
E2=E02ei(wt+j2) (3.2)
Естественно, что результирующая напряженность будет определяться суммой этих колебаний:
|
|
Е=E1+E2 (3.3)
Эта сумма также будет комплексным числом, которое можно представить в виде E=E0ei(wt+j) .
