2018-02-13
283
B математике доказывается общее соотношение, что если спектр функции имеет ширину 
, то время когерентности:
;
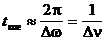Из соотношения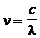 
легко вычислить Dn.
Продиференцируя, получаем: 
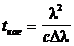
Таким образом мы связали длину когерентности со спектральным составом света.
Пример: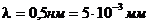 
, после прохождения через светофильтр 
Лазерное излучение: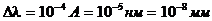 
|
Рис. 3.15 |
Связь длины когерентности и разности хода.
Вернемся к опыту Юнга.
Когда будет наблюдаться интерференция:
1) 
- 
интерференция будет.
2) 
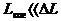- интерференции не будет.
|
Рис. 3.16 |
Для лазерного света это легко достичь. Для естественного приходится строить специальные интерферометры, где добиваются, чтобы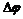 
было близко к нулю, т. е. DL - не превышало несколько длин волн.
