Интерференция в тонких пленках

При падении света на тонкую пленку происходит отражение света от обеих поверхностей пленки. В результате возникают две световые волны, которые при известных условиях могут интерферировать. Разность хода между лучами 1 и 2 до того, как они сойдутся в точке С равна

D_опт = L₂n₂-L₁

Если учесть скачек фазы когда волны отражаются от более плотной среды, то

;

а) Волны 1 и 2 будут интерферировать только в том случае, когда разность хода меньше длины когерентности.

             при l₀=0,5мкм, , .

б) Расстояние между лучами

при               ,  

при               ,     ,

Для солнечного света ,

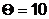Мы приходим к выводу, что в следствии ограничений, накладываемых временной и пространственной когерентностью интерференция при использовании солнечного света наблюдается только в тех случаях, когда толщина пленки не превышает нескольких сотых долей мм.

Интерференция на плоскопараллельной пластинке. (Полосы равного наклона).

Пусть параллельная пластинка освещается рассеянным монохроматическим светом.

Для max:

Для min: =

Каждая полоса образована лучами, падающими на пластинку под одинаковым углом. Поэтому полосы называются полосами равного наклона.

Интерференция на пленке переменной толщины. Пространственная и временная картина ограничивают область, где наблюдается интерференция - это область локализации интерференционных полос.

Положение темных и светлых полос на экране Э зависит теперь от толщины пластинки h¢ и h¢¢. Поэтому такие полосы называются полосами равной толщины. При смещении экрана от клина или к клину начинает сказываться степень пространственной когерентности. Чем больше радиус когерентности тем в большей области можно наблюдать интерференционную картину.

Кольца Ньютона. Классическим примером полос равной толщины являются кольца Ньютона. Они наблюдаются при отражении света от соприкасающихся плоскопараллельной толстой стеклянной пластинки и плосковыпуклой линзы с большим радиусом кривизны.

Свет отражается от верхней грани линзы, нижней, верхней и нижней поверхности пластинки. Однако ввиду малой временной когерентности интерферируют только лучи 2 и 3.

По теореме Пифагора

откуда:

С другой стороны разность хода:

Для темных полос:

Для светлых полос:

Сравнивая D, получим, что в темных полосах

       m = 1,2,3...

в светлых  m =1,2,3...

несложно вычислить и координаты колец

      

или общее условие       m =1,3,5 -темные

m = 2,4,6... светлые

При m = 1 наблюдается нулевое темное кольцо.

В точке соприкосновения наблюдается темное кольцо, обусловленное изменением фазы на , при отражении волны от стекла.

Измеряя радиусы колец нетрудно определить радиус линзы: .