Принцип сохранения области

Теор.1 Мн-во D значений, принимаемых в нек-ой обл-ти G голоморфной ф-ией есть область. Иными словами, голоморфная ф-ия, не тождественная константе, всегда преобразует область в область. (Тут просто ультрамазафакерское доказательствово, так что не стал его включать)                                                                                                               

Следствие(принцип максимума модуля): Ни в одной т.  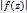голом. ф. f(z) не может иметь максимума

32. Лемма об интегралах по дугам окружностей. Вычисление несобственных интегралов вида _.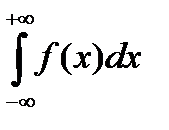

Для достаточно хорошего множества функций  можно вычислить используя теорему о вычетах. Пусть .

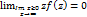Лемма: Пусть f-непрерывна на множестве , и пусть , тогда .

Теор: Пусть функция f-голоморфна в замыкании полуплоскости 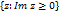 всюду кроме конкретного числа особых точек , лежащих в этой полуплоскости. Если , то

Сл: Пусть f-рациональная ф-я, знаменатель которой не имеет действительных нулей, а степень его не менее чем на 2 единицы больше чем степень числителя, то справедлива ф-я (1).

33. Лемма Жордана. Вычисление интегралов вида .

Лемма Жордана: Пусть f-непрерывная на множестве , для которого 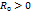 и пусть 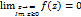, тогда , если .

Теор: Пусть f-голоморфна в замыкании полуплоскости  всюду кроме конечного числа особых точек , лежащих в этой полуплоскости. Если , то

Сл: Если ф-я f(z) при действительном z принимает действительные значения, то в условиях теоремы справедливы формулы:

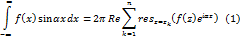
Сл: Пусть f-рациональная ф-я, знаменатель которой не имеет действительных нулей, а степень его не менее чем на 2 единицы больше чем степень числителя. Тогда при  справедливо 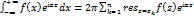. Если, кроме того, f(z) при действительном z действительные значения то справедливы формулы (1), (2).