Пусть Ḋ ϲ 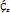 f–голоморфная функция в Ḋ. Совокупность Ḋ и f называется элементами и обозначается {Ḋ,f} при этом Ḋназывают областью элемента. Элемент {
f–голоморфная функция в Ḋ. Совокупность Ḋ и f называется элементами и обозначается {Ḋ,f} при этом Ḋназывают областью элемента. Элемент { 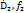 } называют непосредственным аналитическим продолжение элемента {
} называют непосредственным аналитическим продолжение элемента { 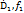 } если: d: =
} если: d: = 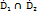 является областью и
является областью и 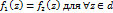 . Из принципа единственности следует что
. Из принципа единственности следует что 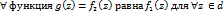 . Таким образом, если элемент {
. Таким образом, если элемент { 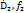 } является непосредственным аналитическим продолжением {
} является непосредственным аналитическим продолжением { 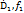 } то это продолжение единственно. Оно обратимо {
} то это продолжение единственно. Оно обратимо { 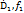 } является непосредственным аналитическим продолжением {
} является непосредственным аналитическим продолжением { 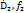 }. Конечное множество элементов {
}. Конечное множество элементов { 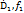 },…, {
},…, { 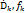 } – называется цепью если элемент {
} – называется цепью если элемент { 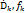 } является непосредственным аналитическим продолжение элемента {
} является непосредственным аналитическим продолжение элемента { 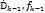 } (k=1,2,3,4,5….,m) При этом говорят что элемент {
} (k=1,2,3,4,5….,m) При этом говорят что элемент { 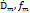 } является аналитическим продолжением элемента {
} является аналитическим продолжением элемента { 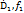 } по соединяющей их цепи области.
} по соединяющей их цепи области.
Принцип симметрии Римана-Шварца.
Пусть две непересекающиеся области 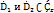 имеют общий участок границы, содержащий кусочно-гладкую простую дугу
имеют общий участок границы, содержащий кусочно-гладкую простую дугу 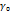 без ее конечных точек. Рассмотрим множество
без ее конечных точек. Рассмотрим множество 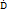 =
= 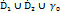 – приставляющее собой область.
– приставляющее собой область.
Лемма
Пусть функция 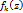 (k=1,2…) голоморфна в области
(k=1,2…) голоморфна в области 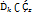 (
(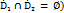 и непрерывна на
и непрерывна на 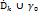 Если
Если 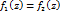 z
z 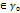 то функция
то функция 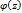 равная
равная 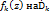 и равная на
и равная на 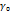 , общее значение является голоморфным в
, общее значение является голоморфным в  .
.
Это лемма будет исполняться в том частном случае когда 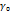 интеграл по прямой, но в этом случае ее справедливость следует из замечания к теореме Мореры.(без доказательства)
интеграл по прямой, но в этом случае ее справедливость следует из замечания к теореме Мореры.(без доказательства)
Теорема (принцип симметрии Римана-Шварца)
Если функция f голоморфна в 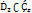 и непрерывна в
и непрерывна в 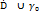 и в точке интеграла
и в точке интеграла 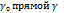 принимает значения принадлежащие интегралу
принимает значения принадлежащие интегралу 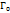 некоторой прямой T
некоторой прямой T 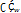 то функция f аналитически продолжается из
то функция f аналитически продолжается из 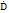 в область
в область 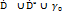 причем значения
причем значения 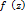 при z
при z 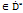 симметричны со значениями
симметричны со значениями 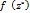 относительно
относительно 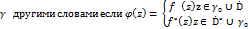 где
где 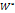 =
= 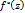 z
z 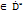 точка симметричная W=
точка симметричная W= 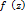 z
z 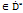 относительно Г, то функция
относительно Г, то функция 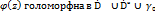 .
.
Доказательство
Повернем плоскости 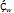 и
и 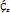 линейным преобразованием z=az+bw=
линейным преобразованием z=az+bw= 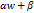 выбрав их так чтобы интеграл
выбрав их так чтобы интеграл 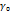 в некоторый интеграл действительной оси плоскости
в некоторый интеграл действительной оси плоскости 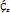 . А примая Г перешла в действительную ось плоскости
. А примая Г перешла в действительную ось плоскости 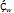 . Эти преобразования сохранили симметрию точек относительно преобразования прямых а также сохранили непрерывность и голоморфность, далее считаем что
. Эти преобразования сохранили симметрию точек относительно преобразования прямых а также сохранили непрерывность и голоморфность, далее считаем что 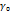 и
и 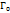 интегралы действительной оси плоскости
интегралы действительной оси плоскости 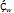 и
и 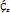 соответственно в окрестности U(
соответственно в окрестности U(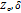 )
) 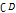 в
в 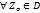 функция fпредставляется степенным рядом.
функция fпредставляется степенным рядом. 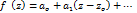
Определим в области 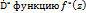 .
. 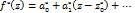
Показав что 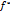 голоморфна в окрестности U(
голоморфна в окрестности U(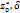 ) т
) т 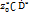 симметрична точке
симметрична точке 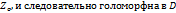 . В силу непрерывности fв
. В силу непрерывности fв 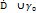 и того что fна
и того что fна 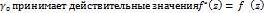 .
.
Теперь легко видеть что 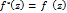 z
z 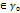 . Согласно лемме функция
. Согласно лемме функция 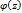 голоморфна в области
голоморфна в области 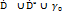 . В этой области
. В этой области 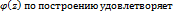 условию
условию 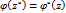 что означает симметрию относительно Г точек zи
что означает симметрию относительно Г точек zи 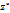 симметричных относительно
симметричных относительно 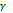 .
. 
 2018-02-13
2018-02-13 217
217








