2018-02-13
373
Распространение теоремы на тот случай когда f имеет конечное число особых точек 
.
Опр: Главные значения от интеграла f(x) на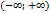 
определены равенством: 
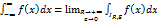, где 
Теор: Пусть f-голоморфна в замыкании полуплоскости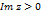 
всюду за исключением конечного числа особых точек 
, лежащих в этой полуплоскости, и конечного числа полюсов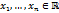 
на действительной оси. Если 
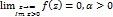, то 
Целые и мероморные функции. Представление рациональной функции в виде суммы многочлена и простейших дробей.
Опр: Ф-я называется целой, если она голоморфна в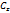 
. Среди элементарных ф-й целыми являются полиномы, показательные, тригонометрические и гиперболические.
Отличная от постоянной целая ф-я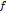 
имеет на 
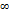или полюс или существует особая точка.
Утв: Целая ф-я с полюсом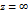 
является полиномом.
Действительно, если 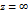- полюс порядка 
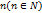, то вычитая главную часть ее ряда Лорана в 
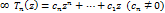получим целую ф-ю 
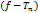с устранимой особенностью на 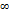, следовательно ограниченную в 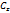. Согласно теореме Лиувилля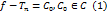 
Итак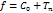 
- полином.
Опр: Целая ф-я с существованием особой точкой на 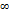называется целой трансцендентной ф-ей.
Утв: Целая трансцендентная ф-ия обозначается бесконечным степенным рядом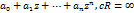 
Более общим, чем класс целых, является класс мероморфных ф-ий.
Опр: Мероморфной называют ф-ию, голоморфную в Сz всюду за исключением точек, в которых f имеет полюсы.
К числу мероморфных относятся рациональные, частное от деления целой на целую.
Теор: f- мероморфная с конечным числом полюсов с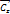 
является рациональной ф-ей.
Замеч: полученная ф-ла (1) дает представление рациональной ф-ии f в виде суммы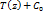 
(целой части) и простейших дробей.
