Пусть голом. в обл. G 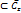 ф-ия f имеет изолир. особую т.
ф-ия f имеет изолир. особую т. 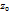 , конечн. или бесконечн. Тогда
, конечн. или бесконечн. Тогда 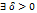 такое, что в
такое, что в 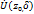 ф-ия f голоморфна. Возьмем в окр.
ф-ия f голоморфна. Возьмем в окр. 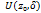 некот. односвяз. обл.G и ограничим спрямляемой замкнут. жорд. кривой.
некот. односвяз. обл.G и ограничим спрямляемой замкнут. жорд. кривой. 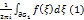 не зависит
не зависит 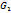 (
(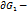 граница области G, ориентир. так, что при движ. по ней, обл. ост.слева).
граница области G, ориентир. так, что при движ. по ней, обл. ост.слева).
Опред.1 Значение инт-ла (1) наз. вычетом ф-ии f в т. 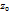 и обозн.
и обозн. 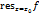 . При нахождении вычета можно считать, что
. При нахождении вычета можно считать, что 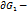 окр-ть с центром в т.
окр-ть с центром в т. 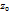 и радиусом
и радиусом  , если
, если 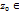
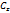 и окр-ть
и окр-ть 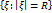 , если
, если 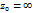 . Пусть
. Пусть 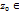
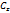 . Разложим ф. f в в
. Разложим ф. f в в 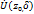 в ряд Лорана:
в ряд Лорана: 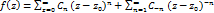 и проинтегр. по
и проинтегр. по 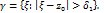 В силу равномерной сх-ти ряда внутри
В силу равномерной сх-ти ряда внутри 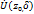 инт-ие ряда по
инт-ие ряда по  можно выполнить почленно. Получим
можно выполнить почленно. Получим 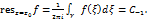 Пусть
Пусть 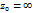 , тогда в нек. окр-ти
, тогда в нек. окр-ти 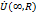 . ф. f разл. в ряд Лорана
. ф. f разл. в ряд Лорана 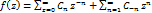 . Его почлен. интегр. по крив.
. Его почлен. интегр. по крив. 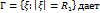
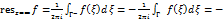
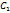 . Итак, вычет ф. в клнечн. изолир. т. z равен коэфф.
. Итак, вычет ф. в клнечн. изолир. т. z равен коэфф. 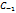 при
при 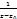 в ряде Лорана этой ф-ии; если же
в ряде Лорана этой ф-ии; если же 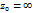 , взятому с противоп. знаком коэфф.
, взятому с противоп. знаком коэфф. 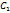 при
при  .
.
Утв. Пусть 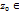
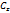 , m-кратность полюса ф. f, тогда
, m-кратность полюса ф. f, тогда 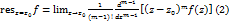 . В частности, если
. В частности, если 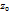 -простой полюс, то
-простой полюс, то 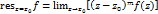 .
.
Замеч. 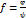 ,
,  ,
, 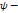 голоморфные ф. в т.
голоморфные ф. в т. 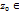
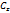 ,
, 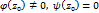 ,
, 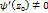 , тогда
, тогда 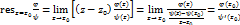
Теоремы Коши о вычетах
Теор.1 Пусть f(z)-ф-ия, голоморфная во всякой т. обл. G, кроме конечного числа особых точек z1,…zn, пусть также Г – спрямл. замкн. контур, содерж. внутри себя точки z1,…zn и целиком лежащ. в обл. G
Док-во: опишем из т. z1,…zn как в центрах окруж. наст. малыми, чтобы они попарно не пересек. и целиком лежали внутри Г, тогда f(z) будет голоморф. в каждой т. замкнут. обл., огранич. сложн. контуром 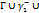 …
… 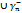 . По теор. Коши
. По теор. Коши 

Теор.2 Пусть ф. f(z) голоморфна в пл. 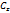 , за исключением конечного числа особых точек z1,…zn, тогда сумма ее вычетов во всех точках z1,…zn и вычета в бескон-ти равна нулю.
, за исключением конечного числа особых точек z1,…zn, тогда сумма ее вычетов во всех точках z1,…zn и вычета в бескон-ти равна нулю.
Док-во: При дост. большом 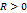 все т. z1,…zn лежат внутри окр-ти
все т. z1,…zn лежат внутри окр-ти 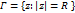 . По теор.1
. По теор.1 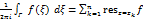 , с другой стороны, этот же интеграл равен
, с другой стороны, этот же интеграл равен 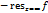 . В итоге
. В итоге 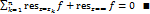
 2018-02-13
2018-02-13 230
230








