Теор.1 В дополнение к условиям теор. Коши предположим, что ф. f не принимает нулевое значение на Г, и каждая т. z1,…zn – полюс ф-ии,тогда 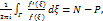 где N-число нулей, P-число полюсов ф. f, лежащих внутри Г, при этом кажд. нуль и кажд. полюс считается столько раз, сколько его кратность.
где N-число нулей, P-число полюсов ф. f, лежащих внутри Г, при этом кажд. нуль и кажд. полюс считается столько раз, сколько его кратность.
Опр. Отношение  наз-ся логарифмич-ой произв-ой ф-ии f,
наз-ся логарифмич-ой произв-ой ф-ии f, 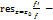 логарифмическим вычетом ф. f в т.
логарифмическим вычетом ф. f в т. 
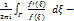 логар. вычетом ф. f относ-но контура Г. Лог. вычет имеет простой смысл, чтобы его раскрыть, перепишем инт-л в виде
логар. вычетом ф. f относ-но контура Г. Лог. вычет имеет простой смысл, чтобы его раскрыть, перепишем инт-л в виде  . Отметим на кривой Г произв. в т.
. Отметим на кривой Г произв. в т. 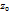 , которую будем считать за нач. и конеч. т. пути интегрирования.
, которую будем считать за нач. и конеч. т. пути интегрирования. 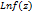 будет непр. меняться и после обхода всей кривой, его значение в т.
будет непр. меняться и после обхода всей кривой, его значение в т. 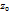 будет отличаться от исх. значений той же т.
будет отличаться от исх. значений той же т. 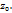 При одном и том же зн-ии
При одном и том же зн-ии 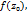 значение
значение  могут различ-ся лишь благодаря разным знач-ям, припис-ым
могут различ-ся лишь благодаря разным знач-ям, припис-ым 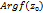 до и после обхода. Обозначая исходное значение аргумента через
до и после обхода. Обозначая исходное значение аргумента через 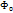 , найдем
, найдем 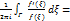
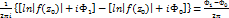 . Отсюда и из теор.1:
. Отсюда и из теор.1:
Теор.2(принцип аргумента) Разность м/у кол-вом нулей и полюсов ф. f(z), заключ-ых внутри замкнут. кривой Г, равна изменению аргумента 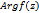 при обходе т. z контура Г по полож. направл-ию, деленному на
при обходе т. z контура Г по полож. направл-ию, деленному на 
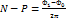
Следствие Если f(z) не имеет полюсов внутри Г, то кол-во нулей ф. f(z), заключ. внутри замк. кривой Г, равно числу полных оборотов вект. f(z) вокруг начала корд. при однократном обходе т. z контура в полож. направл-ии.
Теор Руше.
Теор.1 Если две ф-ии  , голоморфные внутри и на контуре Г, удовл. на Г услов-ям
, голоморфные внутри и на контуре Г, удовл. на Г услов-ям  , то внутри Г ф-ии
, то внутри Г ф-ии 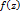 и
и  имеют одинаковое число нулей.
имеют одинаковое число нулей.
Док-во Поскольку  , то
, то 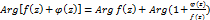 , но
, но 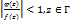 , поэтому конец вектора, изображ.
, поэтому конец вектора, изображ.  , описывает замкнут кривую, целиком заключ. внутри круга с центром в т.1 и радиуса 1. Сл-но, соотв. вектор не делает ни одного оборота вокруг начала координат, и изменение аргумента
, описывает замкнут кривую, целиком заключ. внутри круга с центром в т.1 и радиуса 1. Сл-но, соотв. вектор не делает ни одного оборота вокруг начала координат, и изменение аргумента  при обходе т. z кривой Г равно 0. Измен-ие
при обходе т. z кривой Г равно 0. Измен-ие  совпадает с изм-ем
совпадает с изм-ем 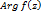 , откуда по принц. аргум-та вытек. рав-во нулей ф-ий
, откуда по принц. аргум-та вытек. рав-во нулей ф-ий 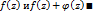
 2018-02-13
2018-02-13 198
198








