Общие свойства преобразования Лапласа (линейность, правила подобия, дифференцирования, смещения, интегрирования)

 

1) Линейность

Пример:

 ;

 ;

 ; ;

 

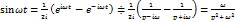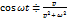2) Теорема подобия

Для  действительно

3) Дифференцирование интеграла

 – непрерывно кусочно-дифф. при  – оригинал, то         

, где

4) Дифференцирование изображения

Д-но, дифф. по переменной р равенства  получим

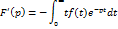
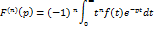
   Пример:

, , , .

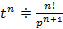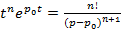5) Интегрирование оригинала

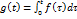Если , то действительно  очевидно явл-ся оригиналом, причем  , положим .

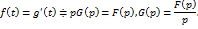
6) Интегрирование изображения

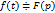 и интеграл – сходится, то , Так как 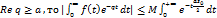 откуда след. равн. сх-ть относит. q в (4).

7) Теорема запаздывания

8) Теорема смещения

Для . Пример: ,

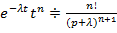
Свёртка оригиналов и её изображение.

Опр. Сверткой функций называется функция .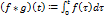

Лемма. Пусть функция двух действительных переменных 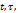абсолютно сходится в пл. и сущ. повторный интеграл 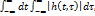тогда .

Теорема умножения. Произведение двух изображений 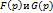 также явл-ся изображением, причем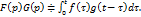

Интеграл Дюамеля.

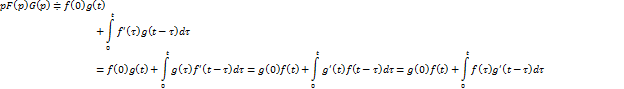
Теоремы разложения.

Теор1. Если функция 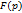 голоморфна в некоторой окрестности бесконечно удаленной точки и ее разложение в ряд имеет вид , 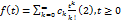то (2) оригинал с разложением F(p).

Теор2. Пусть F(p):

1) Голоморфна всюду, за исключением конечного числа особых точек лежащих в конечной плоскости .

2)

3) 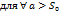абсолютно сходится тогда

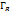Док-во: Применим теор., согласно которой обозначим меру контур, составленный из части лежащей слева от прямой и отрезка этой прямой, соединяющего концы дуги 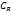. По лемме Жордана при t>0 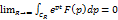, поэтому 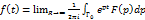. Применяя т. Коши о вычетах, получим (7).

След. Если функция , то ее оригинал полюсы фун. F(p).

Если полюсы простые, то .

 

43. Дискретное преобразование Лапласа. Z-преобразование.

Опр. Z - преобразованием числовой бесконечной посл-ти называется функция F(z) компл. Переменной z, определяемая при рядом Лорана: 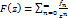и аналитически продолженная в круг |z|<R.

 

44. Применение операционного исчисления к решению дифференциальных уравнений.

Для того чтобы найти x(t) линейного д.у. с постоянными коэфф. , удовлетворяющее начальным условиям: 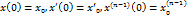следует применить к обоим частям ур-ия преобразования Лапласа:

L(p)X(p)+Q(p)=F(p), где ,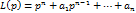

Найдя оригинал для X(p), получим исходное x(t). Аналогично решаются системы.

Пример:

, ;

;

;

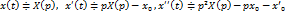Пользуясь таблицей, находим: , где ; 

Частное решение, удовл. начальным условиям: .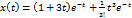

 

N

f(t)

F(p)

N

f(t)

F(p)

1

h (t)

1/ p

6

sin bt

b

p 2+ b 2

2

t n

1 /p n +1

7

chbt

p

p 2- b 2

n!

3

eat

1/ (p - a)

8

shbt

b

p 2- b 2

4

t n

1

9

eat cos bt

p - a

eat

(p - a) n +1

(p - a) 2+ b 2

n!

5

cos bt

p

10

eat sin bt

b

p 2+ b 2

(p - a) 2+ b 2