Дифференциальные уравнения с разделяющимися переменными

 

Уравнения вида:  называется дифференциальным уравнением с разделяющимися переменными.

Подставим

умножим на dx

разделим переменные

разделим на

Замечание: обязательно нужно рассматривать частный случай, когда

переменные разделены

проинтегрируем обе части уравнения

 - общее решение

Дифференциальное уравнение с разделяющимися переменными можно записать в виде:

Отдельный случай !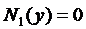

Проинтегрируем обе части уравнения:

Примеры:

1)

2) нач. условия:

 

Однородные дифференциальные уравнения 1 порядка

Определение: Функция  называется однородной порядка n, если

Пример:  - однородная функция порядка n=2

Т.к

Определение: Однородная функция порядка 0 называется однородной.

Определение: Дифференциальное уравнение  называется однородным, если - однородная функция, т.е

Заменим

Таким образом однородное дифференциальное уравнение может быть записано в виде:     

С помощью замены , где t – функция переменной х, однородное дифференциальное уравнение сводится к уравнению с разделяющимися переменными.

Замена

- подставим в уравнение

 

 

Переменные разделены, проинтегрируем обе части уравнения

Сделаем обратную замену, подставив вместо  , получим общее решение в неявном виде.

 

Пример:

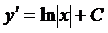
Однородное дифференциальное уравнение может быть записано в дифференциальной форме.

M(x;y)dx+N(x;y)dy=0, где M(x;y) и N(x;y) – однородные функции одинакового порядка.

Разделим на dx и выразим

Пример:

1)