Уравнение неразрывности выражает закон сохранения массы применительно к жидкой среде.
1. Составим баланс массы жидкости в струйке (см. рис. 2.2). Если через сечение 1-1 в единицу времени вошла масса 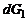 , то за то же время через сечение 2-2 должна выйти масса
, то за то же время через сечение 2-2 должна выйти масса 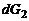 , равная
, равная 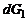 (потери массы через границу струйки отсутствуют). Массу жидкости
(потери массы через границу струйки отсутствуют). Массу жидкости 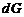 , протекающую через поперечное сечение струйки в единицу времени, называют элементарным массовым расходом.
, протекающую через поперечное сечение струйки в единицу времени, называют элементарным массовым расходом.
Легко убедиться в том, что 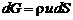 , где
, где 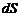 – площадь поперечного сечения струйки. Тогда условие
– площадь поперечного сечения струйки. Тогда условие 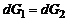 равносильно уравнению
равносильно уравнению
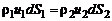 . (2.5)
. (2.5)
Получили уравнение неразрывности для струйки. Если жидкость несжимаема, т.е. 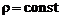 , то
, то 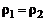 и
и
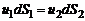 . (2.6)
. (2.6)
 При этом произведение
При этом произведение 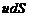 выражает элементарный объемный расход
выражает элементарный объемный расход 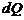 .
.
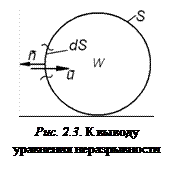
2. Выведем теперь уравнение неразрывности для общего случая движения сплошной среды. Рассмотрим объем 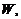 ограниченный поверхностью S (рис. 2.3). Пусть
ограниченный поверхностью S (рис. 2.3). Пусть
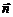 – внешняя нормаль к поверхности, а
– внешняя нормаль к поверхности, а 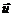 – вектор скорости. Через элемент поверхности dS в единицу времени внутрь объема проникает масса жидкости
– вектор скорости. Через элемент поверхности dS в единицу времени внутрь объема проникает масса жидкости
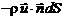 .
.
(учтено, что направления 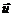 и
и 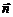 противоположны) Секундная масса, проникающая в объем через всю поверхность, равна
противоположны) Секундная масса, проникающая в объем через всю поверхность, равна
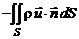 .
.
С другой стороны, приток жидкости в объем приводит к изменению ее массы на величину
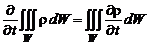 .
.
Очевидно, что изменение массы внутри объема должно быть равно массе, поступившей в него извне, т. е.
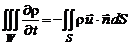 .
.
Применяя теорему Гаусса–Остроградского, получаем:
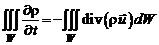 , или
, или 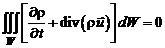 .
.
Ввиду произвольности объема отсюда следует обращение в нуль подынтегрального выражения:
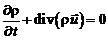 , (2.7а)
, (2.7а)
или
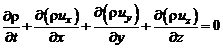 . (2.7б)
. (2.7б)
Это и есть уравнение неразрывности.
Рассмотрим частные случаи.
А) Несжимаемая жидкость ( ):
):
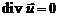 , или
, или 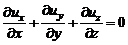 . (2.8)
. (2.8)
Входящие в (2.8) частные производные характеризуют скорость относительного удлинения (укорочения) жидкой частицы. Поэтому если частица удлиняется вдоль двух осей, то она должна укорачиваться относительно третьей оси так, чтобы суммарная скорость деформации оставалась нулевой.
Б) установившееся течение (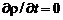 ):
):
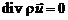 , или
, или 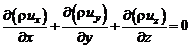 . (2.9)
. (2.9)
 2018-02-14
2018-02-14 373
373








