2018-02-14
1256
Обратимся к записанным ранее условиям равновесия жидкости
.
Если равнодействующая сила 
отлична от нуля, среда начнет двигаться с некоторой скоростью, т.е. в соответствии со вторым законом Ньютона частицы жидкости, составляющие жидкое тело, получат ускорение:
.
Используя выражения для элементарных массовой 
и поверхностной 
сил, приходим к уравнениям движения идеальной жидкости
(2.14а)
или в проекциях на координатные оси
,
, (2.14б)
.
Найдем выражение для вектора ускорения жидкой частицы 
. Согласно подходу Эйлера
,
т.е. полный дифференциал
.
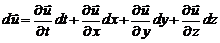Отсюда, разделив обе части на 
и имея в виду, что
, 
, 
,
|
|
|
получим
.
С учетом последнего выражения (2.14) принимает окончательный вид:
(2.15а)
или
,
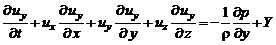, (2.15а)
.
Система уравнений (2.15) также называется уравнениями Эйлера.
Однако для полного описания движения идеальной жидкости этих трех уравнений недостаточно. Для замыкания математической модели используются уравнение неразрывности (2.7), уравнение сохранения энергии в виде 1-го начала термодинамики, уравнение состояния, связывающее давление, плотность и температуру жидкости. На внутренних и внешних границах области течения ставятся граничные условия. Например, на поверхности неподвижного обтекаемого тела нормальная составляющая скорости должна обращаться в нуль. Если изучается неустановившееся течение, то необходимо знать распределения всех гидродинамических величин в начальный момент времени.
В отдельных случаях возможны упрощения модели. Так для описания течения несжимаемой жидкости достаточно использовать уравнения (2.8) и (2.15). В случае адиабатических движений газа уравнение энергии заменяется соотношением
. (2.16)
Уравнение Бернулли
Рассмотрим установившийся поток идеальной жидкости, которая является баротропной средой (в таких средах давление зависит только от плотности, 
). Пусть на жидкость действуют массовые силы консервативной природы (например, сила тяжести). математически это означает, что существует потенциальная функция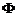 
со свойством
|
|
|
, 
, 
.
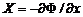В таких условиях уравнения Эйлера (2.15) допускают интеграл. преобразуем систему (2.15б) посредством умножения каждого из уравнений соответственно на 
, 
и 
и почленного их сложения. Тем самым мы проецируем уравнения гидродинамики на линию тока. В левой части имеем
.
Справа получаем
,
где 
– функция давления. Таким образом,
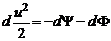либо 
. (2.17)
Это соотношение называют уравнением Бернулли в дифференциальной форме. Его следствием является интеграл Бернулли:
(вдоль линии тока). (2.18)
Частные случаи
А) При движении несжимаемой жидкости в поле силы тяжести (
, 
, 
)
. (2.19)
Б) Для адиабатического течения идеального газа [см. (2.16)]
. (2.20)
Соотношение (2.19) остается справедливым для любой линии тока, проходящей внутри струйки. Поэтому (2.19) можно назвать интегралом Бернулли для струйки идеальной жидкости. Для двух произвольных поперечных сечений струйки можно записать:
. (2.21)
Выясним физический смысл величин, входящих в интеграл Бернулли. Первые два члена выражают удельную потенциальную энергию (положения 
и давления 
), а третий – удельную кинетическую энергию. Следовательно, полная удельная энергия в любом сечении струйки остается неизменной. Другими словами, уравнение Бернулли выражает закон сохранения механической энергии.
В практических приложениях широко используется другая форма уравнения Бернулли – форма напоров. Разделив обе части уравнения (2.21) на ускорение свободного падения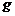 
, получим
. (2.22)
Каждый член (2.22) имеет линейную размерность и выражает
напор, под которым в общем случае понимают высоту столба жидкости, уравновешивающего давление в данной точке. Таким образом,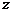 
– геометрический напор, характеризующий положение жидкой частицы над плоскостью отсчета; 
– пьезометрический напор, т. е.– высота столба жидкости, уравновешивающего давление в данной точке; 
– скоростной напор.
Сумма двух первых членов носит название гидростатического напора, а трех – полного либо гидродинамического напора 
. Таким образом, интегралу Бернулли придается геометрическое толкование, которое сводится к следующему. Сумма трех высот: геометрической (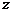), пьезометрической () и скоростной () есть величина постоянная вдоль струйки. Иными словами, полный напор при движении вдоль идеальной струйки остается неизменным.
