Примеры применения интеграла Бернулли

1. Измерения скорости и давления. Рассмотрим обтекание тела потоком невесомой несжимаемой жидкости (рис. 2.4). Параметры потока в сечениях I и II трубки тока связаны уравнением Бернулли

                               ,

где  и  – соответствующие статические и динамические давления.

Рис. 2.4. К измерению скорости и давления в потоке

Сумма 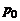 статического и динамического давлений называется полным давлением или давлением торможения и для данной трубки тока является постоянной величиной.

Если сечение 1-1 поместить достаточно далеко, то поток в этом сечении можно считать невозмущенным с параметрами  и . Очевидно, что

                                       .

Отсюда находим скорость невозмущенного потока:

                                  .

Видим, что для определения скорости необходимо измерить полное 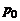 и статическое  давления в набегающем потоке (или их раз­ность).

Для измерения полного давления поток нужно полностью затормо­зить, что и происходит в точке торможения (точка A на рис. 2.4).
С этой же целью можно использовать диск с отверстием, установ­ленный перепендикулярно потоку (рис. 2.5).

Статическое давление – это давление, которое действовало бы на стенку, если бы она двигалась вместе с потоком. Поэтому измерять его нужно на части поверхности тела, расположенной параллельно направлению потока (рис. 2.5).

Рис. 2.5. Приемники полного и статического давлений

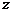2. Скорость истечения жидкости. Определим скорость истечения несжимаемой тяжелой жидкости из большого открытого сосуда через отверстие. Свяжем начало координат с отверстием, в котором , и направим ось  вертикально вверх. Пусть  и  – площади соответственно свободной поверхности жидкости в сосуде и отверстия;
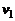 и  – средние скорости жидкости на поверхности и в отверстии.
В данном случае будет справедливо уравнение неразрывности (2.13)

                                          .

Давление на свободной поверхности (при ) будет также равно . Запишем интеграл Бернулли (2.21), связывающий параметры на свободной поверхности и в отверстии:

                                .

Отсюда находим

   , или , т.е. .

Если соотношение  мало, то, пренебрегая в знаменателе слагаемым , получаем для скорости истечения формулу Торичелли

                                          .                                 (2.23)

3. Скорость истечения газа. Рассмотрим установившееся адиабатическое истечение газа из большого закрытого сосуда.Пусть давление и плотность газа в сосуде равны 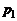 и , атмосферное давление и плотность воздуха –  и . Будем считать, что движение газа происходит в основном вблизи отверстия, а в остальной части сосуда его скорость пренебрежимо мала. Также пренебрегаем силой тяжести. Тогда интеграл (2.20) запишется:

                                ,

откуда

                             .                    (2.24)

Анализируя полученное выражение, видим, что истечение газовой среды возможно только в том случае, если давление газа в сосуде превосходит атмосферное, .