Простой трубопровод постоянного сечения

 

Основным элементом любой трубопроводной системы является простой трубопровод. Трубопровод постоянного диаметра называется простым, если он не имеет ответвлений. Рассмотрим течение жидкости в простом трубопроводе, имеющем длину 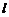, диаметр  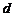и содержащем ряд местных сопротивлений (рис. 3.9). Составим для сечений 1-1 и 2-2 интеграл Бернулли:

                     ,

или

                            ,                   (3.22)

где 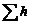 – суммарные потери напора, а коэффициенты Кориолиса  для простоты положили равными единице.

Рис. 3.9. Схема простого трубопровода

 

Введем потребный напор  (если эта величина задана,
то – располагаемый напор ). Статический напор  в правой части (3.22) представим как некоторую эквивалентную высоту  подъема жидкости. Тогда

                                    .                           (3.23)

Потери 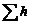 можно выразить следующим образом:

                          ,

где для ламинарного течения

                               ,

[местные сопротивления заменили эквивалентными длинами согласно (3.21)], следовательно,

                            , ;                  (3.24)

для турбулентного течения

                      , ,

следовательно,

                              .                     (3.25)

В итоге (3.23) запишется в виде

                                   .                         (3.26)

Формула (3.26), дополненная (3.24) или (3.25), является основной для расчета простых трубопроводов. По ней можно построить кривую потребного напора (рис. 3.10).

а                                              б

Рис. 3.10. Зависимость потребного напора
от рас­хода жидкости в трубопроводе
при ламинарном (а) и турбулентном (б)
                      течении: 

1 – , 2 – , 3 –

 

Видно, что чем больше расход, который необходимо передавать по трубопроводу, тем больше потребный напор. Величина  положительна, если жидкость поднимается или движется в полость с повышенным давлением, и отрицательна в противных случаях. Точка пересечения кривой потребного напора с осью абсцисс при 0 (точка A на рис. 3.10) определяет расход при движении жидкости самотеком, т.е. за счет лишь разности геометрических высот . В этом случае потребный напор равен нулю, так как давление в начале и в конце трубопровода равно атмосферному; такой трубопровод называют самотечным трубопроводом. Если в конце самотечного трубопровода происходит истечение жидкости в атмосферу, то в уравнении (3.26) к потерям напора следует добавить скоростной напор.

При расчете простых трубопроводов возникают следующие основные задачи.

ЗАДАЧА 1. Дано: расход , давление 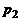, свойства жидкости (  и 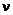), размеры трубопровода, материал и шероховатость трубы. Найти: .

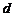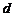Решение. по  и  определяем скорость течения ; по ,  и 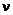 определяем  и режим течения. Затем по соответствующим формулам или опытным данным оцениваем местные сопротивления ; по  и шероховатости находим коэффициент  и проводим расчет  по формуле (3.24).

При ламинарном течении рассчитывать  не обязательно, можно сразу определять 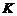 по формуле (3.24).

ЗАДАЧА 2. Дано: располагаемый напор , свойства жидкости, размеры и шероховатость стенок трубопровода. Найти: расход .

Решение: Задаемся режимом течения: сравниваем  с критическим значением , где  
= , и определяем режим течения.

1. При ламинарном течении расход  находим из соотношения (3.23), где вместо  используем . Так как ~ , то задача сводится к решению квадратного уравнения.

2. При турбулентном течении (3.23) явно относительно  не разрешается, так как . В этом случае решаем уравнение (3.23) методом последовательных приближений, графически или численно. В первом методе задаемся начальным значением 0.015…0.040 и из (3.23) находим  и . По  оцениваем значение  и сравниваем его с . Приближения продолжаем до тех пор, пока не добьемся малости величины .

ЗАДАЧА 3. Дано: располагаемый напор  (или ), свойства жидкости, расход, длина и шероховатость трубопровода. Найти: диаметр трубопровода.

Решение. Задаемся режимом течения: сравниваем  с .

1. При ламинарном течении 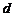 находим по формуле

                                .

Определив 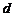, выбираем ближайший стандартный диаметр и по тому же уравнению уточняем значение  при заданном  или наоборот.

2. При турбулентном течении для нахождения 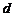 решаем уравнение (3.23) одним из приближенных методов. Например, в методе
последовательных приближений вначале рассчитываем значение скорости :

       ,

где .

Затем определяем потери: , , ,  (или ). Если окажется, что  (или ), то в следующем приближении необходимо увеличить скорость , в противном случае – уменьшить. С этой целью можно воспользоваться формулой . Итерации прекращаем при выполнении условия , где  – заданное малое число (аналогично для ).

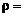Пример 3.1. Пусть 0.1×10⁶ Па, 0.06 м³/с, жидкость Т1 ( 800 кг/м³, 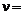2.5×10^–6 м²/с), 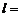30 м, 3×10^–5 м, 6, . Найти диаметр трубопровода.

Решение. Находим 8.45 м/с; 0.095 м,  3.21×10⁵>  – режим течения турбулентный,  
= 0.017,  
= 0.325×10⁶ Па, т. е. 2.25 0.1.
Делаем следующее приближение, корректируя скорость: 4.69 м/с; тогда  
= 0.128 м, 2.4×10⁵, 0.017,  
= 0.088×10⁶ Па, т. е. 0.12 . Повто-
ряем расчет при 4.99 м/с: 0.124 м, 2.33×10⁵, 0.0167, 0.100×10⁶ Па, что с точностью до  совпадает с распола­гаемыми потерями давления.