Истечение из отверстия в тонкой стенке

1. Истечение в газовую среду. Картина установившегося истечения жидкости из сосуда через малое отверстие показана на рис. 4.1. При истечении из отверстия в тонкой стенке криволинейные траектории частиц жидкости сохраняют свою форму и за пределами отверстия, т. е. после выхода из отверстия сечение струи уменьшается и достигает минимальных значений на расстоянии равном ( 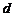– диаметр отверстия).
Таким образом, в сечении В - В будет находиться как называемое сжатое сечение струи жидкости.

Отношение площади сечения струи к площади отверстия называется коэффициентом сжатия ,

, (4.1)

где – площадь отверстия, – площадь сжатого сечения струи.

Рис. 4.1. Схема истечения жидкости в газовую среду

Запишем уравнение Бернулли для двух сечений А - А и В - В:

где 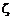– коэффициент сопротивления отверстия. Поскольку величина скоростного напора на свободной поверхности жидкости (сечение А - А) мала из-за малости скорости, ее величиной можно пренебречь.
Тогда

где – расчетный напор. Следовательно, скорость в сжатом сечении струи

. (4.2)

Сомножитель 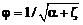в равенстве (4.2) носит название коэффициента скорости.

Зная скорость в сжатом сечении , определим расход жидкости:

, (4.3)

где называется коэффициентом расхода; 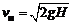– идеальной скоростью истечения [ср. с (2.23)].

2. Типы сжатия струи. Величины коэффициентов отверстия. Если ближайшие стенки и дно сосуда находятся на достаточно большом удалении от отверстия: 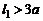, , т.е. не ближе тройного расстояния от направляющих стенок (рис. 4.2), то линии тока вблизи отверстия имеют одинаковую кривизну и сжатие струи называется совершенным.

В иных случаях близко расположенные стенки являются для струи направляющими элементами и ее сжатие будет несовершенным (не одинаковым со всех сторон). В тех случаях, когда сечение отверстия не круглое, сжатие струи будет неполным. При неполном и несовершенном сжатии струи наблюдается некоторое увеличение коэффициента расхода.

При полном совершенном сжатии струи коэффициент сжатия достигает 0.60…0.64. Величины коэффициентов сжатия струи, коэффициента расхода зависят от числа Рейнольдса (рис. 4.3): с возрастанием коэффициент скорости увеличивается, а коэффициент сжатия струи убывает.

Величина коэффициента расхода измеряется простым замером фактического расхода жидкости через отверстие и сопоставлением его с теоретически вычисленным значением:

Коэффициент сжатия струи измеряется по сжатому сечению струи. Коэффициент скорости определяется по траектории струи:

, (4.4)

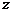где и 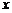– вертикальная и горизонтальная координаты оси струи.

Рис. 4.3. Зависимости коэффициентов расхода,
скорости и сжатия от для круглого
отверстия в тонкой стенке

Пример 4.1. Определить коэффициенты расхода, скорости, сжатия и сопротивления при истечении воды в атмосферу через отверстие диаметром 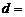10 мм под напором 2 м, если расход 0.294 л/с, а координаты центра одного из сечений струи 2.3 м и 1.2 м.

Решение. Площадь отверстия 7.85∙10^–5 м². Тогда идеальная скорость истечения 6.26 м/с, что соответствует числу Рейнольдса 6.26∙10⁴; коэффициент расхода 0.598. Коэффициент скорости согласно (4.4):
= 0.969. Следовательно, коэффициент сжатия = 0.617. Приняв коэффициент Кориолиса 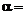1, находим коэффициент сопротивления 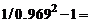0.032.

В области весьма малых ( 25) можно пользоваться теоретической формулой:

Для маловязких жидкостей (воды, бензина, керосина и др.) можно принимать 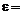0.64, 0.97, 0.62, 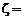0.065.

2. Истечение через затопленное отверстие. Истечение через затопленное отверстие в тонкой стенке, т.е. под уровень жидкости, ничем существенным не отличается от истечения в газовую среду. В этом случае вся кинетическая энергия струи теряется на вихреобразование, как при внезапном расширении.

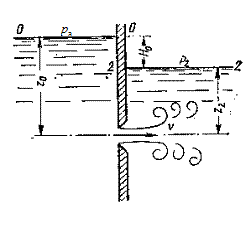
Рис. 4.4. Истечение через затопленное отверстие

Пусть в резервуаре имеется перегородка с отверстием, уровни жидкости находятся на отметках и относительно плоскости сравнения, проходящей через центр тяжести отверстия (рис. 4.4). Запишем уравнение Бернулли для свободных поверхностей жидкости (сечение 0-0 и сечение 2-2), где скорости считаем равными нулю. Учтем при этом, что: