Рассмотрим истечение газа из сосуда неограниченных размеров через малое отверстие с площадью поперечного сечения 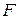 . Параметры состояния внутри сосуда –
. Параметры состояния внутри сосуда – 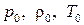 . Определим расход
. Определим расход 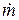 газа при установившемся характере истечения. Обозначим через
газа при установившемся характере истечения. Обозначим через 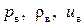 давление, плотность и скорость газа на выходе из отверстия. В качестве исходных уравнений запишем следующее:
давление, плотность и скорость газа на выходе из отверстия. В качестве исходных уравнений запишем следующее:
– условие изоэнтропичности 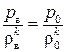 , откуда
, откуда 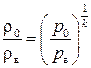 ;
;
– интеграл Бернулли в виде 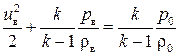 .
.
Тогда скорость истечения газа из сосуда через отверстие равна
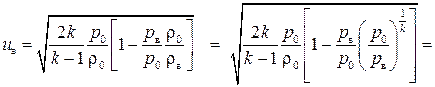
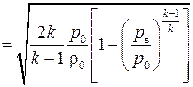 ,
,
а массовый расход газа 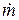 через отверстие определится как
через отверстие определится как
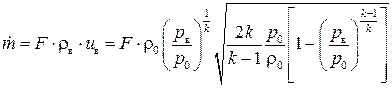 . (3.32)
. (3.32)
Определим, при каком отношении давлений 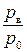 массовый расход имеет максимальное значение
массовый расход имеет максимальное значение 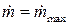 . Возьмем производную от выражения (3.32) и приравняем ее к нулю:
. Возьмем производную от выражения (3.32) и приравняем ее к нулю:
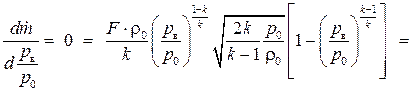
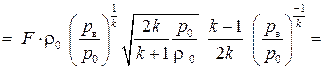
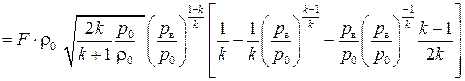 .
.
Очевидно, что максимальное значение расход газа имеет тогда, когда полученная производная обращается в нуль, т. е. когда сомножитель в квадратной скобке последнего выражения равен нулю. Отсюда получаем, что 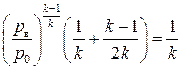 , или
, или 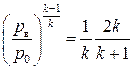 , т. е. максимум расхода достигается при значении отношения давлений
, т. е. максимум расхода достигается при значении отношения давлений
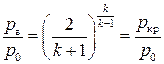 .
.
 Если
Если 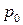 мало отличается от давления окружающей среды
мало отличается от давления окружающей среды 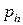 , то давление в струе газа на выходе из отверстия устанавливается равным
, то давление в струе газа на выходе из отверстия устанавливается равным 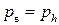 и расход определяется по формуле (3.32). Если далее уменьшать
и расход определяется по формуле (3.32). Если далее уменьшать 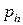 (т. е.
(т. е. 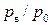 ), то расход будет возрастать (рис. 3.2), достигнув максимума при давлении
), то расход будет возрастать (рис. 3.2), достигнув максимума при давлении 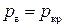 . Дальнейшее понижение
. Дальнейшее понижение 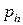 в соответствии с формулой (3.32) должно приводить к уменьшению расхода. В действительности же, как показывают эксперименты, расход остается постоянным и равным максимальному расходу. Следовательно, при величине
в соответствии с формулой (3.32) должно приводить к уменьшению расхода. В действительности же, как показывают эксперименты, расход остается постоянным и равным максимальному расходу. Следовательно, при величине 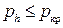 давление на выходе из отверстия всегда равно
давление на выходе из отверстия всегда равно 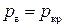 , и
, и 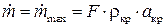 .
.
Элементарное объяснение возникновения
подъемной силы
 Рассмотрим обтекание профиля несжимаемой жидкостью
Рассмотрим обтекание профиля несжимаемой жидкостью  . В передней критической точке О (рис. 3.3) центральная струйка разветвляется на две: ОАВ и ОDВ. Путь ОАВ > ОDВ, а частицы жидкости, разделившись в точке О, должны одновременно встретиться в точке В (в силу уравнения неразрывности). Тогда средняя скорость движения частиц вдоль верней части профиля должна быть больше, чем вдоль нижней (
. В передней критической точке О (рис. 3.3) центральная струйка разветвляется на две: ОАВ и ОDВ. Путь ОАВ > ОDВ, а частицы жидкости, разделившись в точке О, должны одновременно встретиться в точке В (в силу уравнения неразрывности). Тогда средняя скорость движения частиц вдоль верней части профиля должна быть больше, чем вдоль нижней (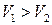 ).
).
Воспользуемся уравнением Бернулли для несжимаемой жидкости 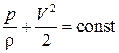 . Записав его для верхней и нижней частей профиля
. Записав его для верхней и нижней частей профиля 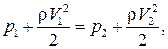 получим, что
получим, что 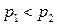 , т. е. давление на нижней стороне профиля больше, чем на верхней. Этот перепад давления и приводит к появлению равнодействующей, направленной вверх, – подъемной силы.
, т. е. давление на нижней стороне профиля больше, чем на верхней. Этот перепад давления и приводит к появлению равнодействующей, направленной вверх, – подъемной силы.
Так как 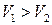 и OAB > ODB, то циркуляция скорости по замкнутому контуру вокруг профиля равна
и OAB > ODB, то циркуляция скорости по замкнутому контуру вокруг профиля равна 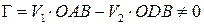 , т. е. еще раз подтверждается вывод, что для создания подъемной силы необходимо, чтобы Г
, т. е. еще раз подтверждается вывод, что для создания подъемной силы необходимо, чтобы Г 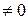 .
.
 2015-03-22
2015-03-22 1529
1529
